from sympy import *
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import pandas as pd
import SymMNA
from IPython.display import display, Markdown, Math, Latex
init_printing()15 2nd Order BRF
This chapter walks through the Python code used to find the transfer function of the circuit shown in Figure 15.1.
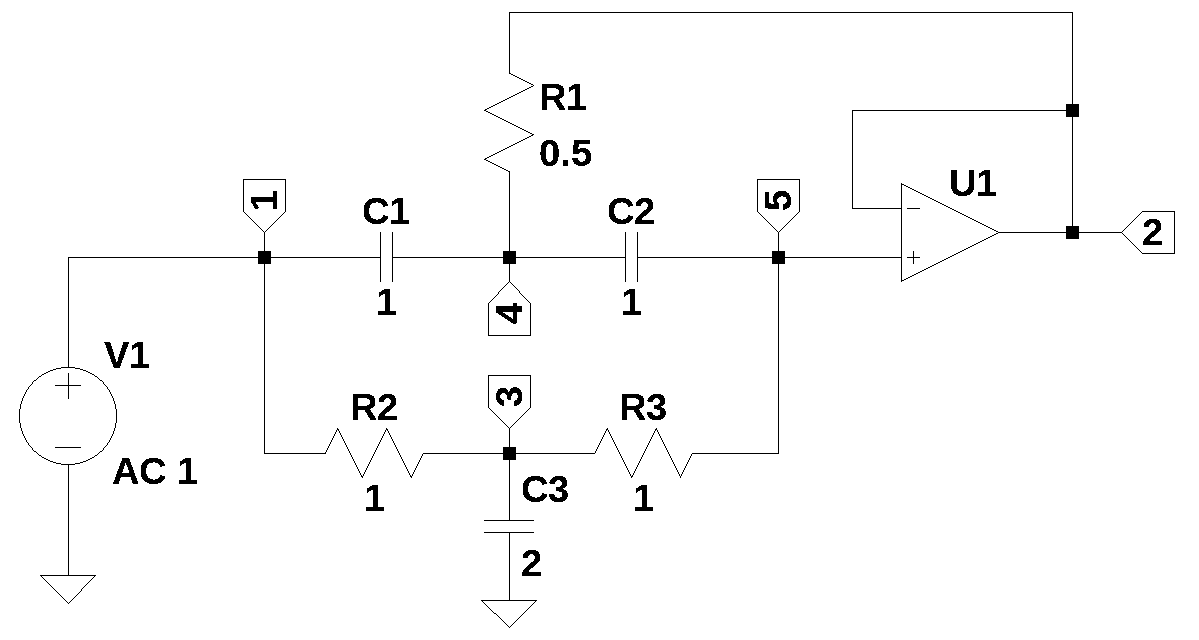
15.1 Circuit description
The circuit above is a 2nd order band reject filter, problem 13-20 from Budak (1974). The schematic of the circuit is shown with each node annotated. The problem asks to obtain the transfer function, \(\frac {V_2} {V_1}\).
The net list for this circuit is:
O1 2 5 2
V1 1 0 1
C3 3 0 2
C1 4 1 1
C2 5 4 1
R1 2 4 0.5
R2 3 1 1
R3 5 3 1The following Python modules are used in this notebook.
15.2 Load the net list
net_list = '''
O1 2 5 2
V1 1 0 1
C3 3 0 2
C1 4 1 1
C2 5 4 1
R1 2 4 0.5
R2 3 1 1
R3 5 3 1
'''15.3 Call the symbolic modified nodal analysis function
report, network_df, i_unk_df, A, X, Z = SymMNA.smna(net_list)15.3.1 Build the network equations
# Put matrices into SymPy
X = Matrix(X)
Z = Matrix(Z)
NE_sym = Eq(A*X,Z)
# display the equations
temp = ''
for i in range(shape(NE_sym.lhs)[0]):
temp += '${:s} = {:s}$<br>'.format(latex(NE_sym.rhs[i]),latex(NE_sym.lhs[i]))
Markdown(temp)\(0 = - C_{1} s v_{4} + I_{V1} + v_{1} \left(C_{1} s + \frac{1}{R_{2}}\right) - \frac{v_{3}}{R_{2}}\)
\(0 = I_{O1} + \frac{v_{2}}{R_{1}} - \frac{v_{4}}{R_{1}}\)
\(0 = v_{3} \left(C_{3} s + \frac{1}{R_{3}} + \frac{1}{R_{2}}\right) - \frac{v_{5}}{R_{3}} - \frac{v_{1}}{R_{2}}\)
\(0 = - C_{1} s v_{1} - C_{2} s v_{5} + v_{4} \left(C_{1} s + C_{2} s + \frac{1}{R_{1}}\right) - \frac{v_{2}}{R_{1}}\)
\(0 = - C_{2} s v_{4} + v_{5} \left(C_{2} s + \frac{1}{R_{3}}\right) - \frac{v_{3}}{R_{3}}\)
\(V_{1} = v_{1}\)
\(0 = v_{2} - v_{5}\)
Turn the free symbols into SymPy variables.
var(str(NE_sym.free_symbols).replace('{','').replace('}',''))\(\displaystyle \left( C_{1}, \ R_{3}, \ R_{1}, \ C_{2}, \ v_{1}, \ v_{4}, \ s, \ v_{2}, \ C_{3}, \ I_{V1}, \ V_{1}, \ I_{O1}, \ v_{5}, \ v_{3}, \ R_{2}\right)\)
15.4 Symbolic solution
U_sym = solve(NE_sym,X)Display the symbolic solution
temp = ''
for i in U_sym.keys():
temp += '${:s} = {:s}$<br>'.format(latex(i),latex(U_sym[i]))
Markdown(temp)\(v_{1} = V_{1}\)
\(v_{2} = \frac{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} V_{1} s^{3} + C_{1} C_{2} R_{1} R_{2} V_{1} s^{2} + C_{1} C_{2} R_{1} R_{3} V_{1} s^{2} + C_{1} R_{1} V_{1} s + C_{2} R_{1} V_{1} s + V_{1}}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + C_{1} C_{2} R_{1} R_{2} s^{2} + C_{1} C_{2} R_{1} R_{3} s^{2} + C_{1} C_{3} R_{1} R_{2} s^{2} + C_{1} R_{1} s + C_{2} C_{3} R_{1} R_{2} s^{2} + C_{2} R_{1} s + C_{3} R_{2} s + 1}\)
\(v_{3} = \frac{C_{1} C_{2} R_{1} R_{2} V_{1} s^{2} + C_{1} C_{2} R_{1} R_{3} V_{1} s^{2} + C_{1} R_{1} V_{1} s + C_{2} R_{1} V_{1} s + V_{1}}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + C_{1} C_{2} R_{1} R_{2} s^{2} + C_{1} C_{2} R_{1} R_{3} s^{2} + C_{1} C_{3} R_{1} R_{2} s^{2} + C_{1} R_{1} s + C_{2} C_{3} R_{1} R_{2} s^{2} + C_{2} R_{1} s + C_{3} R_{2} s + 1}\)
\(v_{4} = \frac{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} V_{1} s^{3} + C_{1} C_{2} R_{1} R_{2} V_{1} s^{2} + C_{1} C_{2} R_{1} R_{3} V_{1} s^{2} + C_{1} C_{3} R_{1} R_{2} V_{1} s^{2} + C_{1} R_{1} V_{1} s + C_{2} R_{1} V_{1} s + V_{1}}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + C_{1} C_{2} R_{1} R_{2} s^{2} + C_{1} C_{2} R_{1} R_{3} s^{2} + C_{1} C_{3} R_{1} R_{2} s^{2} + C_{1} R_{1} s + C_{2} C_{3} R_{1} R_{2} s^{2} + C_{2} R_{1} s + C_{3} R_{2} s + 1}\)
\(v_{5} = \frac{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} V_{1} s^{3} + C_{1} C_{2} R_{1} R_{2} V_{1} s^{2} + C_{1} C_{2} R_{1} R_{3} V_{1} s^{2} + C_{1} R_{1} V_{1} s + C_{2} R_{1} V_{1} s + V_{1}}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + C_{1} C_{2} R_{1} R_{2} s^{2} + C_{1} C_{2} R_{1} R_{3} s^{2} + C_{1} C_{3} R_{1} R_{2} s^{2} + C_{1} R_{1} s + C_{2} C_{3} R_{1} R_{2} s^{2} + C_{2} R_{1} s + C_{3} R_{2} s + 1}\)
\(I_{V1} = \frac{- C_{1} C_{2} C_{3} R_{1} R_{2} V_{1} s^{3} - C_{1} C_{2} C_{3} R_{1} R_{3} V_{1} s^{3} - C_{1} C_{3} R_{1} V_{1} s^{2} - C_{1} C_{3} R_{2} V_{1} s^{2} - C_{2} C_{3} R_{1} V_{1} s^{2} - C_{3} V_{1} s}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + C_{1} C_{2} R_{1} R_{2} s^{2} + C_{1} C_{2} R_{1} R_{3} s^{2} + C_{1} C_{3} R_{1} R_{2} s^{2} + C_{1} R_{1} s + C_{2} C_{3} R_{1} R_{2} s^{2} + C_{2} R_{1} s + C_{3} R_{2} s + 1}\)
\(I_{O1} = \frac{C_{1} C_{3} R_{2} V_{1} s^{2}}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + C_{1} C_{2} R_{1} R_{2} s^{2} + C_{1} C_{2} R_{1} R_{3} s^{2} + C_{1} C_{3} R_{1} R_{2} s^{2} + C_{1} R_{1} s + C_{2} C_{3} R_{1} R_{2} s^{2} + C_{2} R_{1} s + C_{3} R_{2} s + 1}\)
Symbolic form of the transfer function.
H_sym = (U_sym[v2]/U_sym[v1]).simplify().collect(s)
H_sym\(\displaystyle \frac{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + s^{2} \left(C_{1} C_{2} R_{1} R_{2} + C_{1} C_{2} R_{1} R_{3}\right) + s \left(C_{1} R_{1} + C_{2} R_{1}\right) + 1}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3} s^{3} + s^{2} \left(C_{1} C_{2} R_{1} R_{2} + C_{1} C_{2} R_{1} R_{3} + C_{1} C_{3} R_{1} R_{2} + C_{2} C_{3} R_{1} R_{2}\right) + s \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) + 1}\)
The numerator and denominator of the transfer function can be obtained as follows:
num, den = fraction(H_sym)The roots of the numerator can be obtained symbolically. Since the degree of the polynominal is a third order, SymPy can solve for the roots and obtain a solution very quickly. The roots expressed in symbolic form are not very useful, but are easily obtained, something that would be almost impossible to do by hand with pencil and paper.
z = solve(num,s)
z[0]\(\displaystyle - \frac{\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}}{3 \sqrt[3]{\frac{\sqrt{- 4 \left(\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}\right)^{3} + \left(\frac{2 \left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{2}}}{2} + \frac{\left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{2 C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}} - \frac{\sqrt[3]{\frac{\sqrt{- 4 \left(\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}\right)^{3} + \left(\frac{2 \left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{2}}}{2} + \frac{\left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{2 C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}}{3} - \frac{R_{2} + R_{3}}{3 C_{3} R_{2} R_{3}}\)
z[1]\(\displaystyle - \frac{\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}}{3 \left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}\right)^{3} + \left(\frac{2 \left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{2}}}{2} + \frac{\left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{2 C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}} - \frac{\left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}\right)^{3} + \left(\frac{2 \left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{2}}}{2} + \frac{\left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{2 C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}}{3} - \frac{R_{2} + R_{3}}{3 C_{3} R_{2} R_{3}}\)
z[2]\(\displaystyle - \frac{\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}}{3 \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}\right)^{3} + \left(\frac{2 \left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{2}}}{2} + \frac{\left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{2 C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}} - \frac{\left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(\frac{\left(R_{2} + R_{3}\right)^{2}}{C_{3}^{2} R_{2}^{2} R_{3}^{2}} - \frac{3 \left(C_{1} + C_{2}\right)}{C_{1} C_{2} C_{3} R_{2} R_{3}}\right)^{3} + \left(\frac{2 \left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{2}}}{2} + \frac{\left(R_{2} + R_{3}\right)^{3}}{C_{3}^{3} R_{2}^{3} R_{3}^{3}} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} + C_{2}\right) \left(R_{2} + R_{3}\right)}{2 C_{1} C_{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}}{3} - \frac{R_{2} + R_{3}}{3 C_{3} R_{2} R_{3}}\)
The roots of the denominator can be obtained symbolically.
p = solve(den,s)
p[0]\(\displaystyle - \frac{- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}{3 \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{3} + \left(\frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{2 \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}\right)^{2}}}{2} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{2 C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}}} - \frac{\sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{3} + \left(\frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{2 \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}\right)^{2}}}{2} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{2 C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}}}{3} - \frac{C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}}{3 C_{1} C_{2} C_{3} R_{2} R_{3}}\)
p[1]\(\displaystyle - \frac{- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}{3 \left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{3} + \left(\frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{2 \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}\right)^{2}}}{2} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{2 C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}}} - \frac{\left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{3} + \left(\frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{2 \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}\right)^{2}}}{2} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{2 C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}}}{3} - \frac{C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}}{3 C_{1} C_{2} C_{3} R_{2} R_{3}}\)
p[2]\(\displaystyle - \frac{- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}}{3 \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{3} + \left(\frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{2 \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}\right)^{2}}}{2} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{2 C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}}} - \frac{\left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right)}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{2}}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{2}^{2} R_{3}^{2}}\right)^{3} + \left(\frac{27}{C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{2 \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}\right)^{2}}}{2} + \frac{27}{2 C_{1} C_{2} C_{3} R_{1} R_{2} R_{3}} - \frac{9 \left(C_{1} R_{1} + C_{2} R_{1} + C_{3} R_{2}\right) \left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)}{2 C_{1}^{2} C_{2}^{2} C_{3}^{2} R_{1} R_{2}^{2} R_{3}^{2}} + \frac{\left(C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}\right)^{3}}{C_{1}^{3} C_{2}^{3} C_{3}^{3} R_{2}^{3} R_{3}^{3}}}}{3} - \frac{C_{1} C_{2} R_{2} + C_{1} C_{2} R_{3} + C_{1} C_{3} R_{2} + C_{2} C_{3} R_{2}}{3 C_{1} C_{2} C_{3} R_{2} R_{3}}\)
15.5 Numerical solution
Construct a dictionary of element values.
element_values = SymMNA.get_part_values(network_df)
# display the component values
for k,v in element_values.items():
print('{:s} = {:s}'.format(str(k), str(v)))V1 = 1.0
O1 = nan
C3 = 2.0
C1 = 1.0
C2 = 1.0
R1 = 0.5
R2 = 1.0
R3 = 1.0Put the component values into the equations.
NE = NE_sym.subs(element_values)Display the equations with component values.
temp = ''
for i in range(shape(NE.lhs)[0]):
temp += '${:s} = {:s}$<br>'.format(latex(NE.rhs[i]),latex(NE.lhs[i]))
Markdown(temp)\(0 = I_{V1} - 1.0 s v_{4} + v_{1} \cdot \left(1.0 s + 1.0\right) - 1.0 v_{3}\)
\(0 = I_{O1} + 2.0 v_{2} - 2.0 v_{4}\)
\(0 = - 1.0 v_{1} + v_{3} \cdot \left(2.0 s + 2.0\right) - 1.0 v_{5}\)
\(0 = - 1.0 s v_{1} - 1.0 s v_{5} - 2.0 v_{2} + v_{4} \cdot \left(2.0 s + 2.0\right)\)
\(0 = - 1.0 s v_{4} - 1.0 v_{3} + v_{5} \cdot \left(1.0 s + 1.0\right)\)
\(1.0 = v_{1}\)
\(0 = v_{2} - v_{5}\)
Solve for voltages and currents and display the results.
U = solve(NE,X)
temp = ''
for i in U.keys():
temp += '${:s} = {:s}$<br>'.format(latex(i),latex(U[i]))
Markdown(temp)\(v_{1} = 1.0\)
\(v_{2} = \frac{s^{2} + 1.0}{s^{2} + 2.0 s + 1.0}\)
\(v_{3} = \frac{s^{2} + s + 1.0}{s^{3} + 3.0 s^{2} + 3.0 s + 1.0}\)
\(v_{4} = \frac{s^{3} + 2.0 s^{2} + s + 1.0}{s^{3} + 3.0 s^{2} + 3.0 s + 1.0}\)
\(v_{5} = \frac{s^{2} + 1.0}{s^{2} + 2.0 s + 1.0}\)
\(I_{V1} = - \frac{2.0 s}{s + 1.0}\)
\(I_{O1} = \frac{2.0 s^{2}}{s^{3} + 3.0 s^{2} + 3.0 s + 1.0}\)
15.5.1 Plot the frequency response of the transfer function
H = U[v2]/U[v1]
H\(\displaystyle \frac{1.0 \left(s^{2} + 1.0\right)}{s^{2} + 2.0 s + 1.0}\)
num, denom = fraction(H) #returns numerator and denominator
# convert symbolic to numpy polynomial
a = np.array(Poly(num, s).all_coeffs(), dtype=float)
b = np.array(Poly(denom, s).all_coeffs(), dtype=float)
system = (a, b)#x = np.linspace(0.01*2*np.pi, 1*2*np.pi, 2000, endpoint=True)
x = np.logspace(-2, 0, 2000, endpoint=False)*2*np.pi
w, mag, phase = signal.bode(system, w=x) # returns: rad/s, mag in dB, phase in degLoad the csv file of node 10 voltage over the sweep range and plot along with the results obtained from SymPy.
Plot the results.
fig, ax1 = plt.subplots()
ax1.set_ylabel('magnitude, dB')
ax1.set_xlabel('frequency, Hz')
plt.semilogx(w/(2*np.pi), mag,'-b') # Bode magnitude plot
ax1.tick_params(axis='y')
#ax1.set_ylim((-30,20))
plt.grid()
# instantiate a second y-axes that shares the same x-axis
ax2 = ax1.twinx()
color = 'tab:blue'
plt.semilogx(w/(2*np.pi), phase,':',color='tab:red') # Bode phase plot
ax2.set_ylabel('phase, deg',color=color)
ax2.tick_params(axis='y', labelcolor=color)
#ax2.set_ylim((-5,25))
plt.title('Magnitude and phase response')
plt.show()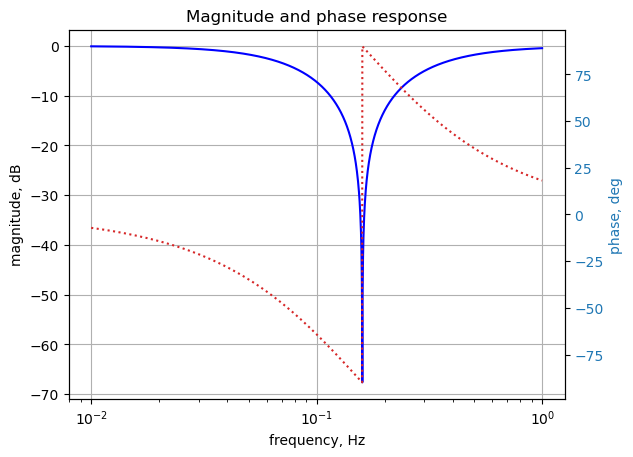
print('null: {:.2f} dB at {:.3f} Hz'.format(mag.min(),w[np.argmin(mag)]/(2*np.pi)))null: -67.66 dB at 0.159 Hz15.5.2 Poles and zeros of the transfer function
The poles and zeros of the transfer function can easly be obtained with the following code:
H_num, H_denom = fraction(H) #returns numerator and denominator
# convert symbolic to numpy polynomial
a = np.array(Poly(H_num, s).all_coeffs(), dtype=float)
b = np.array(Poly(H_denom, s).all_coeffs(), dtype=float)
sys = signal.TransferFunction(a,b)sys_zeros = np.roots(sys.num)
sys_poles = np.roots(sys.den)15.5.2.1 Low pass filter pole zero plot
The poles and zeros of the preamp transfer function are plotted.
plt.plot(np.real(sys_zeros), np.imag(sys_zeros), 'ob', markerfacecolor='none')
plt.plot(np.real(sys_poles), np.imag(sys_poles), 'xr')
plt.legend(['Zeros', 'Poles'], loc=0)
plt.title('Pole / Zero Plot')
plt.xlabel('real part, \u03B1')
plt.ylabel('imaginary part, j\u03C9')
plt.grid()
plt.show()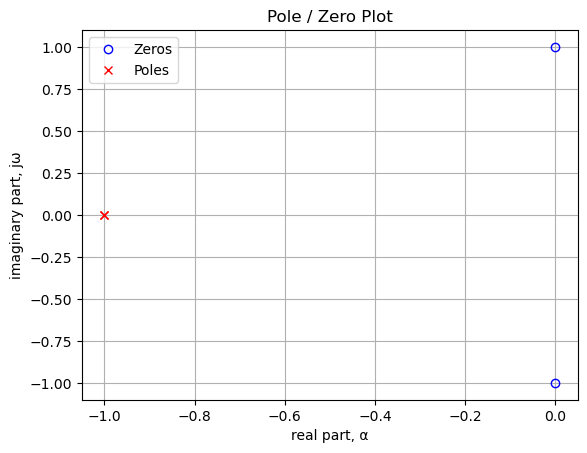
Poles and zeros of the transfer function plotted on the complex plane. The units are in radian frequency.
Printing these values in Hz.
print('number of zeros: {:d}'.format(len(sys_zeros)))
for i in sys_zeros:
print('{:,.2f} Hz'.format(i/(2*np.pi)))number of zeros: 2
0.00+0.16j Hz
0.00-0.16j Hzprint('number of poles: {:d}'.format(len(sys_poles)))
for i in sys_poles:
print('{:,.2f} Hz'.format(i/(2*np.pi)))number of poles: 2
-0.16+0.00j Hz
-0.16-0.00j Hz15.5.3 Impulse and step response
Use the SciPy functions impulse and step to plot the impulse and step response of the system.
plt.subplots(1,2,figsize=(15, 5))
# using subplot function and creating
# plot one
plt.subplot(1, 2, 1)
# impulse response
t, y = signal.impulse(sys,N=500)
plt.plot(t/1e-3, y)
plt.title('Impulse response')
plt.ylabel('volts')
plt.xlabel('time, msec')
plt.grid()
# using subplot function and creating plot two
plt.subplot(1, 2, 2)
t, y = signal.step(sys,N=500)
plt.plot(t/1e-3, y)
plt.title('Step response')
plt.ylabel('volts')
plt.xlabel('time, msec')
plt.grid()
# show plot
plt.show()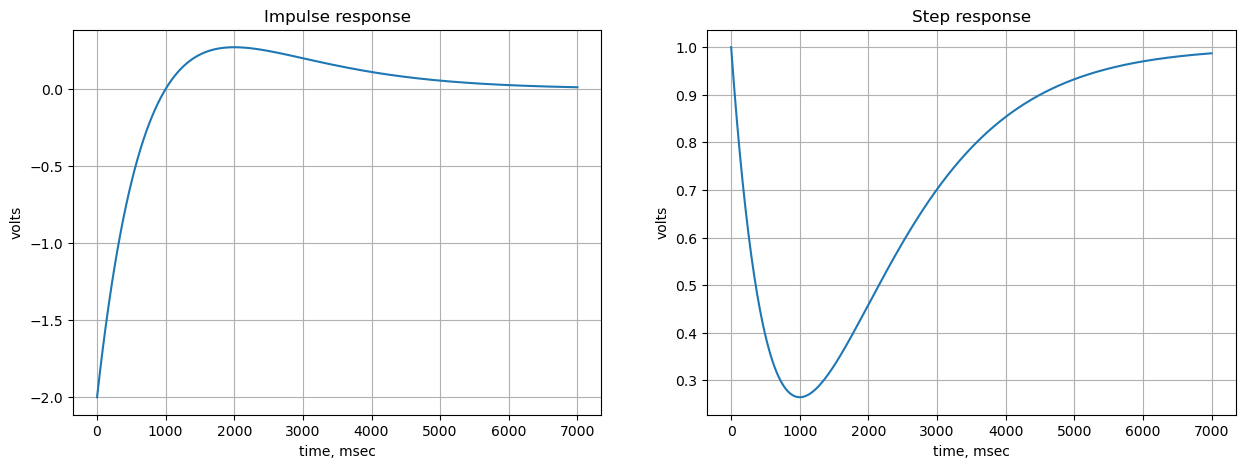
15.5.4 Summary
This chapter is a practical example of how to automate linear circuit analysis. It highlights the power of combining Modified Nodal Analysis with Symbolic Computing to eliminate the tedious algebra involved in traditional circuit design while providing both exact formulas and numerical performance plots. The chapter documents the process of using Python and the SymPy library to derive the symbolic and numerical transfer functions of a specific band-reject (notch) filter circuit.
Performance Visualization:
- Bode Plot: Generates magnitude and phase response plots using
scipy.signal. - Pole-Zero Analysis: Identifies the locations of the poles and zeros to understand filter stability and rejection characteristics.
- Transient Response: Includes sections for calculating the impulse and step responses of the filter.