#import os
from sympy import *
import numpy as np
from tabulate import tabulate
from scipy import signal
import matplotlib.pyplot as plt
import pandas as pd
import SymMNA
from IPython.display import display, Markdown, Math, Latex
init_printing()37 Test 7
This test circuit shown in Figure 37.1 is a large circuit with 53 branches, 28 nodes and at least two of each element type except for Op Amps. This circuit is designed to stress the Python code with a large number of variables and unknowns.
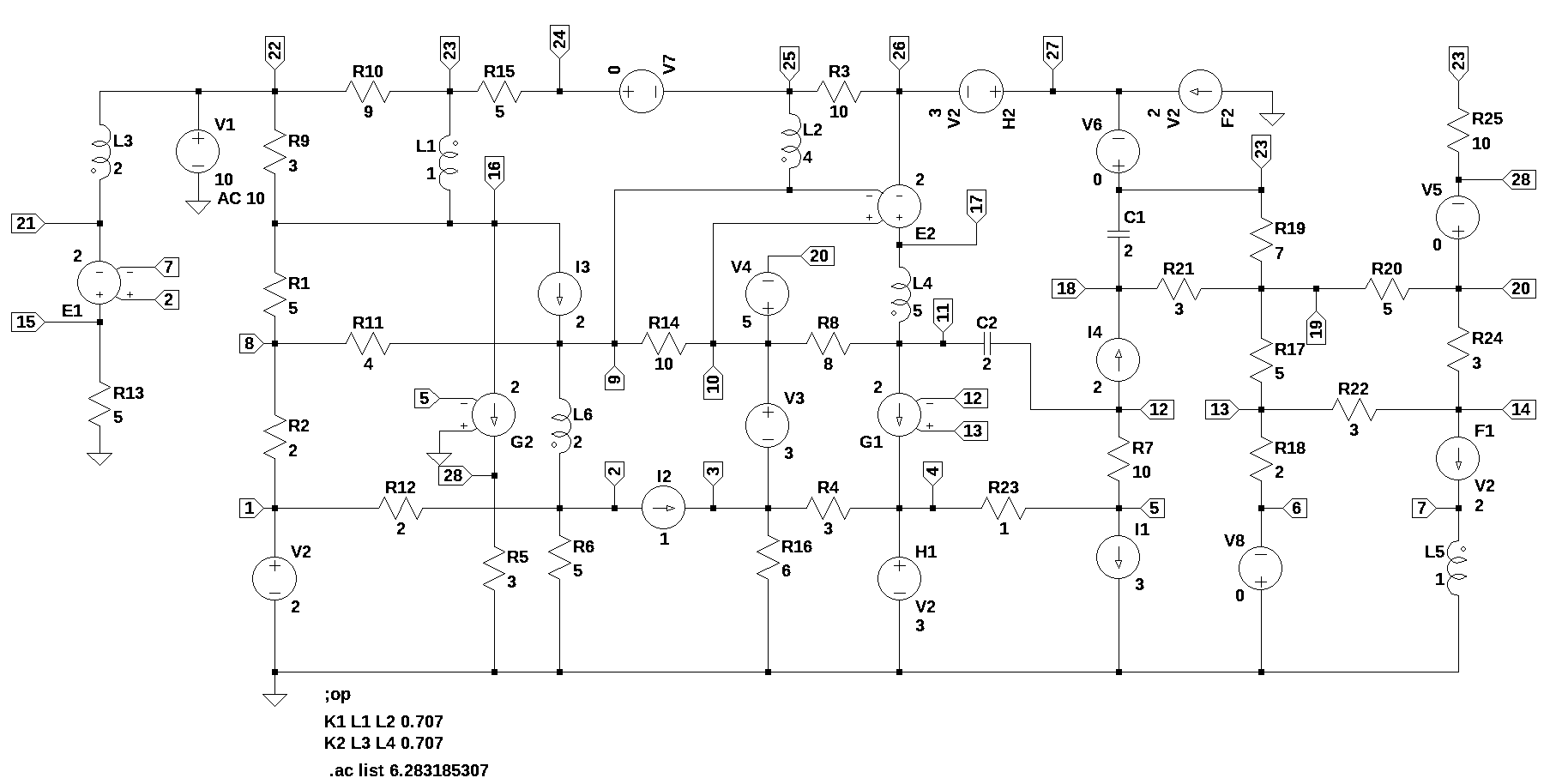
The netlist generated by LTSpice:
R1 16 8 5
R2 8 1 2
R6 2 0 5
R8 11 10 8
R10 23 22 9
R11 9 8 4
R12 2 1 2
R14 10 9 10
R15 24 23 5
V1 22 0 10 AC 10
V2 1 0 2
V3 10 3 3
V4 10 20 5
I1 5 0 3
I2 2 3 1
I3 16 9 2
I4 12 18 2
R7 12 5 10
R16 3 0 6
R3 26 25 10
R4 4 3 3
F1 14 7 V2 2
E1 15 21 2 7 2
H1 4 0 V2 3
G1 11 4 13 12 2
L1 16 23 1 Rser=0
L2 25 9 4 Rser=0
V5 20 28 0
V6 23 27 0
L3 22 21 2 Rser=0
L4 17 11 5 Rser=0
C1 23 18 2
C2 12 11 2
L5 0 7 1 Rser=0
L6 9 2 2 Rser=0
F2 0 27 V2 2
E2 17 26 10 9 2
H2 27 26 V2 3
G2 16 28 0 5 2
V7 24 25 0
V8 0 6 0
R9 22 16 3
R13 15 0 5
R17 19 13 5
R18 13 6 2
R19 23 19 7
R20 20 19 5
R21 19 18 3
R22 14 13 3
R23 5 4 1
R24 20 14 3
R25 23 28 10
R5 28 0 3
K1 L1 L2 0.707
K2 L3 L4 0.70737.1 Load the net list
net_list = '''
R1 16 8 5
R2 8 1 2
R6 2 0 5
R8 11 10 8
R10 23 22 9
R11 9 8 4
R12 2 1 2
R14 10 9 10
R15 24 23 5
V1 22 0 10
V2 1 0 2
V3 10 3 3
V4 10 20 5
I1 5 0 3
I2 2 3 1
I3 16 9 2
I4 12 18 2
R7 12 5 10
R16 3 0 6
R3 26 25 10
R4 4 3 3
F1 14 7 V2 2
E1 15 21 2 7 2
H1 4 0 V2 3
G1 11 4 13 12 2
L1 16 23 1
L2 25 9 4
V5 20 28 0
V6 23 27 0
L3 22 21 2
L4 17 11 5
C1 23 18 2
C2 12 11 2
L5 0 7 1
L6 9 2 2
F2 0 27 V2 2
E2 17 26 10 9 2
H2 27 26 V2 3
G2 16 28 0 5 2
V7 24 25 0
V8 0 6 0
R9 22 16 3
R13 15 0 5
R17 19 13 5
R18 13 6 2
R19 23 19 7
R20 20 19 5
R21 19 18 3
R22 14 13 3
R23 5 4 1
R24 20 14 3
R25 23 28 10
R5 28 0 3
K1 L1 L2 0.707
K2 L3 L4 0.707
'''37.2 Call the symbolic modified nodal analysis function
report, network_df, i_unk_df, A, X, Z = SymMNA.smna(net_list)Display the equations
# reform X and Z into Matrix type for printing
Xp = Matrix(X)
Zp = Matrix(Z)
temp = ''
for i in range(len(X)):
temp += '${:s}$<br>'.format(latex(Eq((A*Xp)[i:i+1][0],Zp[i])))
Markdown(temp)\(I_{V2} + v_{1} \cdot \left(\frac{1}{R_{2}} + \frac{1}{R_{12}}\right) - \frac{v_{8}}{R_{2}} - \frac{v_{2}}{R_{12}} = 0\)
\(- I_{L6} + v_{2} \cdot \left(\frac{1}{R_{6}} + \frac{1}{R_{12}}\right) - \frac{v_{1}}{R_{12}} = - I_{2}\)
\(- I_{V3} + v_{3} \cdot \left(\frac{1}{R_{4}} + \frac{1}{R_{16}}\right) - \frac{v_{4}}{R_{4}} = I_{2}\)
\(I_{H1} + g_{1} v_{12} - g_{1} v_{13} + v_{4} \cdot \left(\frac{1}{R_{4}} + \frac{1}{R_{23}}\right) - \frac{v_{3}}{R_{4}} - \frac{v_{5}}{R_{23}} = 0\)
\(v_{5} \cdot \left(\frac{1}{R_{7}} + \frac{1}{R_{23}}\right) - \frac{v_{12}}{R_{7}} - \frac{v_{4}}{R_{23}} = - I_{1}\)
\(- I_{V8} - \frac{v_{13}}{R_{18}} + \frac{v_{6}}{R_{18}} = 0\)
\(- I_{F1} - I_{L5} = 0\)
\(v_{8} \cdot \left(\frac{1}{R_{2}} + \frac{1}{R_{11}} + \frac{1}{R_{1}}\right) - \frac{v_{1}}{R_{2}} - \frac{v_{9}}{R_{11}} - \frac{v_{16}}{R_{1}} = 0\)
\(- I_{L2} + I_{L6} + v_{9} \cdot \left(\frac{1}{R_{14}} + \frac{1}{R_{11}}\right) - \frac{v_{10}}{R_{14}} - \frac{v_{8}}{R_{11}} = I_{3}\)
\(I_{V3} + I_{V4} + v_{10} \cdot \left(\frac{1}{R_{8}} + \frac{1}{R_{14}}\right) - \frac{v_{11}}{R_{8}} - \frac{v_{9}}{R_{14}} = 0\)
\(- I_{L4} + g_{1} v_{13} + v_{11} \left(C_{2} s + \frac{1}{R_{8}}\right) + v_{12} \left(- C_{2} s - g_{1}\right) - \frac{v_{10}}{R_{8}} = 0\)
\(- C_{2} s v_{11} + v_{12} \left(C_{2} s + \frac{1}{R_{7}}\right) - \frac{v_{5}}{R_{7}} = - I_{4}\)
\(v_{13} \cdot \left(\frac{1}{R_{22}} + \frac{1}{R_{18}} + \frac{1}{R_{17}}\right) - \frac{v_{14}}{R_{22}} - \frac{v_{6}}{R_{18}} - \frac{v_{19}}{R_{17}} = 0\)
\(I_{F1} + v_{14} \cdot \left(\frac{1}{R_{24}} + \frac{1}{R_{22}}\right) - \frac{v_{20}}{R_{24}} - \frac{v_{13}}{R_{22}} = 0\)
\(I_{Ea1} + \frac{v_{15}}{R_{13}} = 0\)
\(I_{L1} - g_{2} v_{5} + v_{16} \cdot \left(\frac{1}{R_{9}} + \frac{1}{R_{1}}\right) - \frac{v_{22}}{R_{9}} - \frac{v_{8}}{R_{1}} = - I_{3}\)
\(I_{Ea2} + I_{L4} = 0\)
\(- C_{1} s v_{23} + v_{18} \left(C_{1} s + \frac{1}{R_{21}}\right) - \frac{v_{19}}{R_{21}} = I_{4}\)
\(v_{19} \cdot \left(\frac{1}{R_{21}} + \frac{1}{R_{20}} + \frac{1}{R_{19}} + \frac{1}{R_{17}}\right) - \frac{v_{18}}{R_{21}} - \frac{v_{20}}{R_{20}} - \frac{v_{23}}{R_{19}} - \frac{v_{13}}{R_{17}} = 0\)
\(- I_{V4} + I_{V5} + v_{20} \cdot \left(\frac{1}{R_{24}} + \frac{1}{R_{20}}\right) - \frac{v_{14}}{R_{24}} - \frac{v_{19}}{R_{20}} = 0\)
\(- I_{Ea1} - I_{L3} = 0\)
\(I_{L3} + I_{V1} + v_{22} \cdot \left(\frac{1}{R_{9}} + \frac{1}{R_{10}}\right) - \frac{v_{16}}{R_{9}} - \frac{v_{23}}{R_{10}} = 0\)
\(- C_{1} s v_{18} - I_{L1} + I_{V6} + v_{23} \left(C_{1} s + \frac{1}{R_{25}} + \frac{1}{R_{19}} + \frac{1}{R_{15}} + \frac{1}{R_{10}}\right) - \frac{v_{28}}{R_{25}} - \frac{v_{19}}{R_{19}} - \frac{v_{24}}{R_{15}} - \frac{v_{22}}{R_{10}} = 0\)
\(I_{V7} - \frac{v_{23}}{R_{15}} + \frac{v_{24}}{R_{15}} = 0\)
\(I_{L2} - I_{V7} + \frac{v_{25}}{R_{3}} - \frac{v_{26}}{R_{3}} = 0\)
\(- I_{Ea2} - I_{H2} - \frac{v_{25}}{R_{3}} + \frac{v_{26}}{R_{3}} = 0\)
\(- I_{F2} + I_{H2} - I_{V6} = 0\)
\(- I_{V5} + g_{2} v_{5} + v_{28} \cdot \left(\frac{1}{R_{5}} + \frac{1}{R_{25}}\right) - \frac{v_{23}}{R_{25}} = 0\)
\(v_{22} = V_{1}\)
\(v_{1} = V_{2}\)
\(v_{10} - v_{3} = V_{3}\)
\(v_{10} - v_{20} = V_{4}\)
\(v_{20} - v_{28} = V_{5}\)
\(v_{23} - v_{27} = V_{6}\)
\(v_{24} - v_{25} = V_{7}\)
\(- v_{6} = V_{8}\)
\(I_{F1} - I_{V2} f_{1} = 0\)
\(- ea_{1} v_{2} + ea_{1} v_{7} + v_{15} - v_{21} = 0\)
\(- I_{V2} h_{1} + v_{4} = 0\)
\(- I_{L1} L_{1} s - I_{L2} M_{1} s + v_{16} - v_{23} = 0\)
\(- I_{L1} M_{1} s - I_{L2} L_{2} s + v_{25} - v_{9} = 0\)
\(- I_{L3} L_{3} s - I_{L4} M_{2} s - v_{21} + v_{22} = 0\)
\(- I_{L3} M_{2} s - I_{L4} L_{4} s - v_{11} + v_{17} = 0\)
\(- I_{L5} L_{5} s - v_{7} = 0\)
\(- I_{L6} L_{6} s - v_{2} + v_{9} = 0\)
\(I_{F2} - I_{V2} f_{2} = 0\)
\(- ea_{2} v_{10} + ea_{2} v_{9} + v_{17} - v_{26} = 0\)
\(- I_{V2} h_{2} - v_{26} + v_{27} = 0\)
37.2.1 Netlist statistics
print(report)Net list report
number of lines in netlist: 55
number of branches: 53
number of nodes: 28
number of unknown currents: 20
number of RLC (passive components): 33
number of inductors: 6
number of independent voltage sources: 8
number of independent current sources: 4
number of Op Amps: 0
number of E - VCVS: 2
number of G - VCCS: 2
number of F - CCCS: 2
number of H - CCVS: 2
number of K - Coupled inductors: 2
37.2.2 Connectivity Matrix
A\(\displaystyle \left[\begin{array}{cccccccccccccccccccccccccccccccccccccccccccccccc}\frac{1}{R_{2}} + \frac{1}{R_{12}} & - \frac{1}{R_{12}} & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{2}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\- \frac{1}{R_{12}} & \frac{1}{R_{6}} + \frac{1}{R_{12}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0\\0 & 0 & \frac{1}{R_{4}} + \frac{1}{R_{16}} & - \frac{1}{R_{4}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & - \frac{1}{R_{4}} & \frac{1}{R_{4}} + \frac{1}{R_{23}} & - \frac{1}{R_{23}} & 0 & 0 & 0 & 0 & 0 & 0 & g_{1} & - g_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & - \frac{1}{R_{23}} & \frac{1}{R_{7}} + \frac{1}{R_{23}} & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{7}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & \frac{1}{R_{18}} & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{18}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0\\- \frac{1}{R_{2}} & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{R_{2}} + \frac{1}{R_{11}} + \frac{1}{R_{1}} & - \frac{1}{R_{11}} & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{1}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{11}} & \frac{1}{R_{14}} + \frac{1}{R_{11}} & - \frac{1}{R_{14}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{14}} & \frac{1}{R_{8}} + \frac{1}{R_{14}} & - \frac{1}{R_{8}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{8}} & C_{2} s + \frac{1}{R_{8}} & - C_{2} s - g_{1} & g_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & - \frac{1}{R_{7}} & 0 & 0 & 0 & 0 & 0 & - C_{2} s & C_{2} s + \frac{1}{R_{7}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{18}} & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{R_{22}} + \frac{1}{R_{18}} + \frac{1}{R_{17}} & - \frac{1}{R_{22}} & 0 & 0 & 0 & 0 & - \frac{1}{R_{17}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{22}} & \frac{1}{R_{24}} + \frac{1}{R_{22}} & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{24}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{R_{13}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & - g_{2} & 0 & 0 & - \frac{1}{R_{1}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{R_{9}} + \frac{1}{R_{1}} & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{9}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & C_{1} s + \frac{1}{R_{21}} & - \frac{1}{R_{21}} & 0 & 0 & 0 & - C_{1} s & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{17}} & 0 & 0 & 0 & 0 & - \frac{1}{R_{21}} & \frac{1}{R_{21}} + \frac{1}{R_{20}} + \frac{1}{R_{19}} + \frac{1}{R_{17}} & - \frac{1}{R_{20}} & 0 & 0 & - \frac{1}{R_{19}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{24}} & 0 & 0 & 0 & 0 & - \frac{1}{R_{20}} & \frac{1}{R_{24}} + \frac{1}{R_{20}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{9}} & 0 & 0 & 0 & 0 & 0 & \frac{1}{R_{9}} + \frac{1}{R_{10}} & - \frac{1}{R_{10}} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - C_{1} s & - \frac{1}{R_{19}} & 0 & 0 & - \frac{1}{R_{10}} & C_{1} s + \frac{1}{R_{25}} + \frac{1}{R_{19}} + \frac{1}{R_{15}} + \frac{1}{R_{10}} & - \frac{1}{R_{15}} & 0 & 0 & 0 & - \frac{1}{R_{25}} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{15}} & \frac{1}{R_{15}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{R_{3}} & - \frac{1}{R_{3}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{3}} & \frac{1}{R_{3}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & -1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 1\\0 & 0 & 0 & 0 & g_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{1}{R_{25}} & 0 & 0 & 0 & 0 & \frac{1}{R_{5}} + \frac{1}{R_{25}} & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - f_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & - ea_{1} & 0 & 0 & 0 & 0 & ea_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - h_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - L_{1} s & - M_{1} s & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - M_{1} s & - L_{2} s & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - L_{3} s & - M_{2} s & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - M_{2} s & - L_{4} s & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - L_{5} s & 0 & 0 & 0 & 0\\0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - L_{6} s & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - f_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & ea_{2} & - ea_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0 & - h_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right]\)
37.2.3 Unknown voltages and currents
X\(\displaystyle \left[ v_{1}, \ v_{2}, \ v_{3}, \ v_{4}, \ v_{5}, \ v_{6}, \ v_{7}, \ v_{8}, \ v_{9}, \ v_{10}, \ v_{11}, \ v_{12}, \ v_{13}, \ v_{14}, \ v_{15}, \ v_{16}, \ v_{17}, \ v_{18}, \ v_{19}, \ v_{20}, \ v_{21}, \ v_{22}, \ v_{23}, \ v_{24}, \ v_{25}, \ v_{26}, \ v_{27}, \ v_{28}, \ I_{V1}, \ I_{V2}, \ I_{V3}, \ I_{V4}, \ I_{V5}, \ I_{V6}, \ I_{V7}, \ I_{V8}, \ I_{F1}, \ I_{Ea1}, \ I_{H1}, \ I_{L1}, \ I_{L2}, \ I_{L3}, \ I_{L4}, \ I_{L5}, \ I_{L6}, \ I_{F2}, \ I_{Ea2}, \ I_{H2}\right]\)
37.2.4 Known voltages and currents
Z\(\displaystyle \left[ 0, \ - I_{2}, \ I_{2}, \ 0, \ - I_{1}, \ 0, \ 0, \ 0, \ I_{3}, \ 0, \ 0, \ - I_{4}, \ 0, \ 0, \ 0, \ - I_{3}, \ 0, \ I_{4}, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ V_{1}, \ V_{2}, \ V_{3}, \ V_{4}, \ V_{5}, \ V_{6}, \ V_{7}, \ V_{8}, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0, \ 0\right]\)
37.2.5 Network dataframe
network_df| element | p node | n node | cp node | cn node | Vout | value | Vname | Lname1 | Lname2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | V1 | 22 | 0 | NaN | NaN | NaN | 10.0 | NaN | NaN | NaN |
| 1 | V2 | 1 | 0 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 2 | V3 | 10 | 3 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 3 | V4 | 10 | 20 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 4 | V5 | 20 | 28 | NaN | NaN | NaN | 0.0 | NaN | NaN | NaN |
| 5 | V6 | 23 | 27 | NaN | NaN | NaN | 0.0 | NaN | NaN | NaN |
| 6 | V7 | 24 | 25 | NaN | NaN | NaN | 0.0 | NaN | NaN | NaN |
| 7 | V8 | 0 | 6 | NaN | NaN | NaN | 0.0 | NaN | NaN | NaN |
| 8 | R1 | 16 | 8 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 9 | R2 | 8 | 1 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 10 | R6 | 2 | 0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 11 | R8 | 11 | 10 | NaN | NaN | NaN | 8.0 | NaN | NaN | NaN |
| 12 | R10 | 23 | 22 | NaN | NaN | NaN | 9.0 | NaN | NaN | NaN |
| 13 | R11 | 9 | 8 | NaN | NaN | NaN | 4.0 | NaN | NaN | NaN |
| 14 | R12 | 2 | 1 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 15 | R14 | 10 | 9 | NaN | NaN | NaN | 10.0 | NaN | NaN | NaN |
| 16 | R15 | 24 | 23 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 17 | I1 | 5 | 0 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 18 | I2 | 2 | 3 | NaN | NaN | NaN | 1.0 | NaN | NaN | NaN |
| 19 | I3 | 16 | 9 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 20 | I4 | 12 | 18 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 21 | R7 | 12 | 5 | NaN | NaN | NaN | 10.0 | NaN | NaN | NaN |
| 22 | R16 | 3 | 0 | NaN | NaN | NaN | 6.0 | NaN | NaN | NaN |
| 23 | R3 | 26 | 25 | NaN | NaN | NaN | 10.0 | NaN | NaN | NaN |
| 24 | R4 | 4 | 3 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 25 | F1 | 14 | 7 | NaN | NaN | NaN | 2.0 | V2 | NaN | NaN |
| 26 | Ea1 | 15 | 21 | 2 | 7 | NaN | 2.0 | NaN | NaN | NaN |
| 27 | H1 | 4 | 0 | NaN | NaN | NaN | 3.0 | V2 | NaN | NaN |
| 28 | G1 | 11 | 4 | 13 | 12 | NaN | 2.0 | NaN | NaN | NaN |
| 29 | L1 | 16 | 23 | NaN | NaN | NaN | 1.0 | NaN | NaN | NaN |
| 30 | L2 | 25 | 9 | NaN | NaN | NaN | 4.0 | NaN | NaN | NaN |
| 31 | L3 | 22 | 21 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 32 | L4 | 17 | 11 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 33 | C1 | 23 | 18 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 34 | C2 | 12 | 11 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 35 | L5 | 0 | 7 | NaN | NaN | NaN | 1.0 | NaN | NaN | NaN |
| 36 | L6 | 9 | 2 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 37 | F2 | 0 | 27 | NaN | NaN | NaN | 2.0 | V2 | NaN | NaN |
| 38 | Ea2 | 17 | 26 | 10 | 9 | NaN | 2.0 | NaN | NaN | NaN |
| 39 | H2 | 27 | 26 | NaN | NaN | NaN | 3.0 | V2 | NaN | NaN |
| 40 | G2 | 16 | 28 | 0 | 5 | NaN | 2.0 | NaN | NaN | NaN |
| 41 | R9 | 22 | 16 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 42 | R13 | 15 | 0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 43 | R17 | 19 | 13 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 44 | R18 | 13 | 6 | NaN | NaN | NaN | 2.0 | NaN | NaN | NaN |
| 45 | R19 | 23 | 19 | NaN | NaN | NaN | 7.0 | NaN | NaN | NaN |
| 46 | R20 | 20 | 19 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN |
| 47 | R21 | 19 | 18 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 48 | R22 | 14 | 13 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 49 | R23 | 5 | 4 | NaN | NaN | NaN | 1.0 | NaN | NaN | NaN |
| 50 | R24 | 20 | 14 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 51 | R25 | 23 | 28 | NaN | NaN | NaN | 10.0 | NaN | NaN | NaN |
| 52 | R5 | 28 | 0 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN |
| 53 | K1 | NaN | NaN | NaN | NaN | NaN | 0.707 | NaN | L1 | L2 |
| 54 | K2 | NaN | NaN | NaN | NaN | NaN | 0.707 | NaN | L3 | L4 |
37.2.6 Unknown current dataframe
i_unk_df| element | p node | n node | |
|---|---|---|---|
| 0 | V1 | 22 | 0 |
| 1 | V2 | 1 | 0 |
| 2 | V3 | 10 | 3 |
| 3 | V4 | 10 | 20 |
| 4 | V5 | 20 | 28 |
| 5 | V6 | 23 | 27 |
| 6 | V7 | 24 | 25 |
| 7 | V8 | 0 | 6 |
| 8 | F1 | 14 | 7 |
| 9 | Ea1 | 15 | 21 |
| 10 | H1 | 4 | 0 |
| 11 | L1 | 16 | 23 |
| 12 | L2 | 25 | 9 |
| 13 | L3 | 22 | 21 |
| 14 | L4 | 17 | 11 |
| 15 | L5 | 0 | 7 |
| 16 | L6 | 9 | 2 |
| 17 | F2 | 0 | 27 |
| 18 | Ea2 | 17 | 26 |
| 19 | H2 | 27 | 26 |
37.2.7 Build the network equations
# Put matrices into SymPy
X = Matrix(X)
Z = Matrix(Z)
NE_sym = Eq(A*X,Z)Turn the free symbols into SymPy variables.
var(str(NE_sym.free_symbols).replace('{','').replace('}',''))\(\displaystyle \left( v_{19}, \ M_{1}, \ L_{5}, \ I_{Ea2}, \ R_{14}, \ R_{13}, \ I_{L4}, \ s, \ h_{1}, \ v_{18}, \ I_{V1}, \ I_{F1}, \ R_{10}, \ I_{H2}, \ I_{V3}, \ v_{11}, \ I_{V5}, \ v_{12}, \ v_{15}, \ R_{17}, \ L_{6}, \ g_{2}, \ v_{7}, \ I_{L6}, \ v_{9}, \ V_{7}, \ v_{3}, \ I_{F2}, \ R_{16}, \ v_{1}, \ R_{9}, \ v_{4}, \ v_{27}, \ I_{2}, \ C_{2}, \ L_{4}, \ R_{12}, \ v_{23}, \ R_{18}, \ v_{21}, \ ea_{1}, \ L_{2}, \ V_{1}, \ v_{17}, \ g_{1}, \ h_{2}, \ I_{H1}, \ I_{V2}, \ L_{1}, \ R_{11}, \ R_{24}, \ R_{2}, \ I_{V4}, \ R_{21}, \ R_{15}, \ f_{2}, \ v_{6}, \ I_{L5}, \ R_{19}, \ V_{3}, \ R_{1}, \ I_{1}, \ f_{1}, \ I_{Ea1}, \ v_{10}, \ I_{V8}, \ v_{28}, \ V_{2}, \ L_{3}, \ R_{25}, \ M_{2}, \ ea_{2}, \ I_{4}, \ R_{3}, \ R_{5}, \ R_{4}, \ R_{8}, \ R_{22}, \ v_{5}, \ R_{7}, \ I_{V7}, \ v_{26}, \ V_{6}, \ v_{25}, \ R_{6}, \ v_{8}, \ R_{23}, \ v_{2}, \ v_{13}, \ v_{22}, \ R_{20}, \ V_{4}, \ I_{L1}, \ v_{16}, \ I_{V6}, \ v_{24}, \ I_{L2}, \ v_{20}, \ V_{8}, \ C_{1}, \ V_{5}, \ I_{3}, \ I_{L3}, \ v_{14}\right)\)
37.3 Symbolic solution
The symbolic solution was taking longer than a couple of minutes on my i3-8130U CPU @ 2.20GHz, so I interruped the kernel and commended the code.
#U_sym = solve(NE_sym,X)Display the symbolic solution
#temp = ''
#for i in U_sym.keys():
# temp += '${:s} = {:s}$<br>'.format(latex(i),latex(U_sym[i]))
#Markdown(temp)37.4 Construct a dictionary of element values
element_values = SymMNA.get_part_values(network_df)
# display the component values
for k,v in element_values.items():
print('{:s} = {:s}'.format(str(k), str(v)))V1 = 10.0
V2 = 2.0
V3 = 3.0
V4 = 5.0
V5 = 0.0
V6 = 0.0
V7 = 0.0
V8 = 0.0
R1 = 5.0
R2 = 2.0
R6 = 5.0
R8 = 8.0
R10 = 9.0
R11 = 4.0
R12 = 2.0
R14 = 10.0
R15 = 5.0
I1 = 3.0
I2 = 1.0
I3 = 2.0
I4 = 2.0
R7 = 10.0
R16 = 6.0
R3 = 10.0
R4 = 3.0
f1 = 2.0
ea1 = 2.0
h1 = 3.0
g1 = 2.0
L1 = 1.0
L2 = 4.0
L3 = 2.0
L4 = 5.0
C1 = 2.0
C2 = 2.0
L5 = 1.0
L6 = 2.0
f2 = 2.0
ea2 = 2.0
h2 = 3.0
g2 = 2.0
R9 = 3.0
R13 = 5.0
R17 = 5.0
R18 = 2.0
R19 = 7.0
R20 = 5.0
R21 = 3.0
R22 = 3.0
R23 = 1.0
R24 = 3.0
R25 = 10.0
R5 = 3.0
K1 = 0.707
K2 = 0.70737.4.1 Mutual inductance
In the netlist, the line below specifies that L3 and L4 are connected by a magnetic circuit. >K1 L1 L2 0.707
K2 L3 L4 0.707
K1 identifies the mutual inductance between in two inductors, L3 and L4. k is the coefficient of coupling.
A coupled inductor has two or more windings that are connected by a magnetic circuit. Coupled inductors transfer energy from one winding to a different winding usually through a commonly used core. The efficiency of the magnetic coupling between both the windings is defined by the coupling factor k or by mutual inductance.
The coupling constant and the mutual inductance are related by the equation:
\(k = \frac {M}{\sqrt{L_1 \times L_2}}\)
Where k is the coupling coefficient and in spice the value of k can be from -1 to +1 to account for a a negative phase relation. Phase dots are drawn on the schematic to indicate the relative direction of the windings. In LTspice the phase dots are associated with the negative terminal of the winding.
K1, K2 = symbols('K1 K2')
# calculate the coupling constant from the mutual inductance
element_values[M1] = element_values[K1]*np.sqrt(element_values[L1] *element_values[L2])
print('mutual inductance, M1 = {:.9f}'.format(element_values[M1]))
element_values[M2] = element_values[K2]*np.sqrt(element_values[L3] *element_values[L4])
print('mutual inductance, M2 = {:.9f}'.format(element_values[M2]))mutual inductance, M1 = 1.414000000
mutual inductance, M2 = 2.23573030637.5 DC operating point
NE = NE_sym.subs(element_values)
NE_dc = NE.subs({s:0})Display the equations with numeric values.
temp = ''
for i in range(shape(NE_dc.lhs)[0]):
temp += '${:s} = {:s}$<br>'.format(latex(NE_dc.rhs[i]),latex(NE_dc.lhs[i]))
Markdown(temp)\(0 = I_{V2} + 1.0 v_{1} - 0.5 v_{2} - 0.5 v_{8}\)
\(-1.0 = - I_{L6} - 0.5 v_{1} + 0.7 v_{2}\)
\(1.0 = - I_{V3} + 0.5 v_{3} - 0.333333333333333 v_{4}\)
\(0 = I_{H1} + 2.0 v_{12} - 2.0 v_{13} - 0.333333333333333 v_{3} + 1.33333333333333 v_{4} - 1.0 v_{5}\)
\(-3.0 = - 0.1 v_{12} - 1.0 v_{4} + 1.1 v_{5}\)
\(0 = - I_{V8} - 0.5 v_{13} + 0.5 v_{6}\)
\(0 = - I_{F1} - I_{L5}\)
\(0 = - 0.5 v_{1} - 0.2 v_{16} + 0.95 v_{8} - 0.25 v_{9}\)
\(2.0 = - I_{L2} + I_{L6} - 0.1 v_{10} - 0.25 v_{8} + 0.35 v_{9}\)
\(0 = I_{V3} + I_{V4} + 0.225 v_{10} - 0.125 v_{11} - 0.1 v_{9}\)
\(0 = - I_{L4} - 0.125 v_{10} + 0.125 v_{11} - 2.0 v_{12} + 2.0 v_{13}\)
\(-2.0 = 0.1 v_{12} - 0.1 v_{5}\)
\(0 = 1.03333333333333 v_{13} - 0.333333333333333 v_{14} - 0.2 v_{19} - 0.5 v_{6}\)
\(0 = I_{F1} - 0.333333333333333 v_{13} + 0.666666666666667 v_{14} - 0.333333333333333 v_{20}\)
\(0 = I_{Ea1} + 0.2 v_{15}\)
\(-2.0 = I_{L1} + 0.533333333333333 v_{16} - 0.333333333333333 v_{22} - 2.0 v_{5} - 0.2 v_{8}\)
\(0 = I_{Ea2} + I_{L4}\)
\(2.0 = 0.333333333333333 v_{18} - 0.333333333333333 v_{19}\)
\(0 = - 0.2 v_{13} - 0.333333333333333 v_{18} + 0.876190476190476 v_{19} - 0.2 v_{20} - 0.142857142857143 v_{23}\)
\(0 = - I_{V4} + I_{V5} - 0.333333333333333 v_{14} - 0.2 v_{19} + 0.533333333333333 v_{20}\)
\(0 = - I_{Ea1} - I_{L3}\)
\(0 = I_{L3} + I_{V1} - 0.333333333333333 v_{16} + 0.444444444444444 v_{22} - 0.111111111111111 v_{23}\)
\(0 = - I_{L1} + I_{V6} - 0.142857142857143 v_{19} - 0.111111111111111 v_{22} + 0.553968253968254 v_{23} - 0.2 v_{24} - 0.1 v_{28}\)
\(0 = I_{V7} - 0.2 v_{23} + 0.2 v_{24}\)
\(0 = I_{L2} - I_{V7} + 0.1 v_{25} - 0.1 v_{26}\)
\(0 = - I_{Ea2} - I_{H2} - 0.1 v_{25} + 0.1 v_{26}\)
\(0 = - I_{F2} + I_{H2} - I_{V6}\)
\(0 = - I_{V5} - 0.1 v_{23} + 0.433333333333333 v_{28} + 2.0 v_{5}\)
\(10.0 = v_{22}\)
\(2.0 = v_{1}\)
\(3.0 = v_{10} - v_{3}\)
\(5.0 = v_{10} - v_{20}\)
\(0 = v_{20} - v_{28}\)
\(0 = v_{23} - v_{27}\)
\(0 = v_{24} - v_{25}\)
\(0 = - v_{6}\)
\(0 = I_{F1} - 2.0 I_{V2}\)
\(0 = v_{15} - 2.0 v_{2} - v_{21} + 2.0 v_{7}\)
\(0 = - 3.0 I_{V2} + v_{4}\)
\(0 = v_{16} - v_{23}\)
\(0 = v_{25} - v_{9}\)
\(0 = - v_{21} + v_{22}\)
\(0 = - v_{11} + v_{17}\)
\(0 = - v_{7}\)
\(0 = - v_{2} + v_{9}\)
\(0 = I_{F2} - 2.0 I_{V2}\)
\(0 = - 2.0 v_{10} + v_{17} - v_{26} + 2.0 v_{9}\)
\(0 = - 3.0 I_{V2} - v_{26} + v_{27}\)
Solve for voltages and currents.
U_dc = solve(NE_dc,X)Display the numerical solution
Six significant digits are displayed so that results can be compared to LTSpice.
table_header = ['unknown', 'mag']
table_row = []
for name, value in U_dc.items():
table_row.append([str(name),float(value)])
print(tabulate(table_row, headers=table_header,colalign = ('left','decimal'),tablefmt="simple",floatfmt=('5s','.6f')))unknown mag
--------- ----------
v1 2.000000
v2 5.971750
v3 -10.279202
v4 13.605119
v5 8.605119
v6 0.000000
v7 0.000000
v8 7.098329
v9 5.971750
v10 -7.279202
v11 -18.854648
v12 -11.394881
v13 -7.101000
v14 -23.295220
v15 21.943500
v16 21.252375
v17 -18.854648
v18 8.136867
v19 2.136867
v20 -12.279202
v21 10.000000
v22 10.000000
v23 21.252375
v24 5.971750
v25 5.971750
v26 7.647256
v27 21.252375
v28 -12.279202
I_V1 0.612356
I_V2 4.535040
I_V3 -10.674641
I_V4 10.552805
I_V5 9.764013
I_V6 -1.761697
I_V7 3.056125
I_V8 3.550500
I_F1 9.070079
I_Ea1 -4.388700
I_H1 -4.373678
I_L1 8.628637
I_L2 3.223676
I_L3 4.388700
I_L4 7.140832
I_L5 -9.070079
I_L6 4.180225
I_F2 9.070079
I_Ea2 -7.140832
I_H2 7.308382The node voltages and current through the sources are solved for. The Sympy generated solution matches the LTSpice results:
--- Operating Point ---
V(16): 21.2524 voltage
V(8): 7.09833 voltage
V(1): 2 voltage
V(2): 5.97175 voltage
V(11): -18.8546 voltage
V(10): -7.2792 voltage
V(23): 21.2524 voltage
V(22): 10 voltage
V(9): 5.97175 voltage
V(24): 5.97175 voltage
V(3): -10.2792 voltage
V(20): -12.2792 voltage
V(5): 8.60512 voltage
V(12): -11.3949 voltage
V(18): 8.13687 voltage
V(26): 7.64726 voltage
V(25): 5.97175 voltage
V(4): 13.6051 voltage
V(14): -23.2952 voltage
V(7): 0 voltage
V(15): 21.9435 voltage
V(21): 10 voltage
V(13): -7.101 voltage
V(28): -12.2792 voltage
V(27): 21.2524 voltage
V(17): -18.8546 voltage
V(6): 0 voltage
V(19): 2.13687 voltage
I(C1): 2.6231e-11 device_current
I(C2): 1.49195e-11 device_current
I(F1): 9.07008 device_current
I(F2): 9.07008 device_current
I(H1): -4.37368 device_current
I(H2): 7.30838 device_current
I(L1): 8.62864 device_current
I(L2): 3.22368 device_current
I(L3): 4.3887 device_current
I(L4): 7.14083 device_current
I(L5): -9.07008 device_current
I(L6): 4.18022 device_current
I(I1): 3 device_current
I(I2): 1 device_current
I(I3): 2 device_current
I(I4): 2 device_current
I(R1): 2.83081 device_current
I(R2): 2.54916 device_current
I(R6): 1.19435 device_current
I(R8): -1.44693 device_current
I(R10): 1.25026 device_current
I(R11): -0.281645 device_current
I(R12): 1.98588 device_current
I(R14): -1.3251 device_current
I(R15): -3.05612 device_current
I(R7): -2 device_current
I(R16): -1.7132 device_current
I(R3): 0.167551 device_current
I(R4): 7.96144 device_current
I(R9): -3.75079 device_current
I(R13): 4.3887 device_current
I(R17): 1.84757 device_current
I(R18): -3.5505 device_current
I(R19): 2.73079 device_current
I(R20): -2.88321 device_current
I(R21): -2 device_current
I(R22): -5.39807 device_current
I(R23): -5 device_current
I(R24): 3.67201 device_current
I(R25): 3.35316 device_current
I(R5): -4.09307 device_current
I(G1): 8.58776 device_current
I(G2): -17.2102 device_current
I(E1): -4.3887 device_current
I(E2): -7.14083 device_current
I(V1): 0.612356 device_current
I(V2): 4.53504 device_current
I(V3): -10.6746 device_current
I(V4): 10.5528 device_current
I(V5): 9.76401 device_current
I(V6): -1.7617 device_current
I(V7): 3.05612 device_current
I(V8): 3.5505 device_current
The results from LTSpice agree with the SymPy results.
37.5.1 AC analysis
Solve equations for \(\omega\) equal to 1 radian per second, s = 1j. V1 is the AC source, magnitude of 10
V2, V3, V4, I1, I2, I3, I4 are DC sources and are set to zero for AC analysis.
element_values[V2] = 0
element_values[V3] = 0
element_values[V4] = 0
element_values[I1] = 0
element_values[I2] = 0
element_values[I3] = 0
element_values[I4] = 0
NE = NE_sym.subs(element_values)
NE_w1 = NE.subs({s:1j})Display the equations with numeric values.
temp = ''
for i in range(shape(NE_w1.lhs)[0]):
temp += '${:s} = {:s}$<br>'.format(latex(NE_w1.rhs[i]),latex(NE_w1.lhs[i]))
Markdown(temp)\(0 = I_{V2} + 1.0 v_{1} - 0.5 v_{2} - 0.5 v_{8}\)
\(0 = - I_{L6} - 0.5 v_{1} + 0.7 v_{2}\)
\(0 = - I_{V3} + 0.5 v_{3} - 0.333333333333333 v_{4}\)
\(0 = I_{H1} + 2.0 v_{12} - 2.0 v_{13} - 0.333333333333333 v_{3} + 1.33333333333333 v_{4} - 1.0 v_{5}\)
\(0 = - 0.1 v_{12} - 1.0 v_{4} + 1.1 v_{5}\)
\(0 = - I_{V8} - 0.5 v_{13} + 0.5 v_{6}\)
\(0 = - I_{F1} - I_{L5}\)
\(0 = - 0.5 v_{1} - 0.2 v_{16} + 0.95 v_{8} - 0.25 v_{9}\)
\(0 = - I_{L2} + I_{L6} - 0.1 v_{10} - 0.25 v_{8} + 0.35 v_{9}\)
\(0 = I_{V3} + I_{V4} + 0.225 v_{10} - 0.125 v_{11} - 0.1 v_{9}\)
\(0 = - I_{L4} - 0.125 v_{10} + v_{11} \cdot \left(0.125 + 2.0 i\right) + v_{12} \left(-2.0 - 2.0 i\right) + 2.0 v_{13}\)
\(0 = - 2.0 i v_{11} + v_{12} \cdot \left(0.1 + 2.0 i\right) - 0.1 v_{5}\)
\(0 = 1.03333333333333 v_{13} - 0.333333333333333 v_{14} - 0.2 v_{19} - 0.5 v_{6}\)
\(0 = I_{F1} - 0.333333333333333 v_{13} + 0.666666666666667 v_{14} - 0.333333333333333 v_{20}\)
\(0 = I_{Ea1} + 0.2 v_{15}\)
\(0 = I_{L1} + 0.533333333333333 v_{16} - 0.333333333333333 v_{22} - 2.0 v_{5} - 0.2 v_{8}\)
\(0 = I_{Ea2} + I_{L4}\)
\(0 = v_{18} \cdot \left(0.333333333333333 + 2.0 i\right) - 0.333333333333333 v_{19} - 2.0 i v_{23}\)
\(0 = - 0.2 v_{13} - 0.333333333333333 v_{18} + 0.876190476190476 v_{19} - 0.2 v_{20} - 0.142857142857143 v_{23}\)
\(0 = - I_{V4} + I_{V5} - 0.333333333333333 v_{14} - 0.2 v_{19} + 0.533333333333333 v_{20}\)
\(0 = - I_{Ea1} - I_{L3}\)
\(0 = I_{L3} + I_{V1} - 0.333333333333333 v_{16} + 0.444444444444444 v_{22} - 0.111111111111111 v_{23}\)
\(0 = - I_{L1} + I_{V6} - 2.0 i v_{18} - 0.142857142857143 v_{19} - 0.111111111111111 v_{22} + v_{23} \cdot \left(0.553968253968254 + 2.0 i\right) - 0.2 v_{24} - 0.1 v_{28}\)
\(0 = I_{V7} - 0.2 v_{23} + 0.2 v_{24}\)
\(0 = I_{L2} - I_{V7} + 0.1 v_{25} - 0.1 v_{26}\)
\(0 = - I_{Ea2} - I_{H2} - 0.1 v_{25} + 0.1 v_{26}\)
\(0 = - I_{F2} + I_{H2} - I_{V6}\)
\(0 = - I_{V5} - 0.1 v_{23} + 0.433333333333333 v_{28} + 2.0 v_{5}\)
\(10.0 = v_{22}\)
\(0 = v_{1}\)
\(0 = v_{10} - v_{3}\)
\(0 = v_{10} - v_{20}\)
\(0 = v_{20} - v_{28}\)
\(0 = v_{23} - v_{27}\)
\(0 = v_{24} - v_{25}\)
\(0 = - v_{6}\)
\(0 = I_{F1} - 2.0 I_{V2}\)
\(0 = v_{15} - 2.0 v_{2} - v_{21} + 2.0 v_{7}\)
\(0 = - 3.0 I_{V2} + v_{4}\)
\(0 = - 1.0 i I_{L1} - 1.414 i I_{L2} + v_{16} - v_{23}\)
\(0 = - 1.414 i I_{L1} - 4.0 i I_{L2} + v_{25} - v_{9}\)
\(0 = - 2.0 i I_{L3} - 2.23573030573904 i I_{L4} - v_{21} + v_{22}\)
\(0 = - 2.23573030573904 i I_{L3} - 5.0 i I_{L4} - v_{11} + v_{17}\)
\(0 = - 1.0 i I_{L5} - v_{7}\)
\(0 = - 2.0 i I_{L6} - v_{2} + v_{9}\)
\(0 = I_{F2} - 2.0 I_{V2}\)
\(0 = - 2.0 v_{10} + v_{17} - v_{26} + 2.0 v_{9}\)
\(0 = - 3.0 I_{V2} - v_{26} + v_{27}\)
Solve for voltages and currents.
U_w1 = solve(NE_w1,X)Display the numerical solution
Six significant digits are displayed so that results can be compared to LTSpice.
table_header = ['unknown', 'mag','phase, deg']
table_row = []
for name, value in U_w1.items():
table_row.append([str(name),float(abs(value)),float(arg(value)*180/np.pi)])
print(tabulate(table_row, headers=table_header,colalign = ('left','decimal','decimal'),tablefmt="simple",floatfmt=('5s','.6f','.6f')))unknown mag phase, deg
--------- --------- ------------
v1 0.000000 nan
v2 1.269063 -156.737432
v3 5.563110 92.699863
v4 5.822884 -82.858298
v5 5.049515 -83.161299
v6 0.000000 nan
v7 3.881923 7.141702
v8 3.734176 -63.802595
v9 2.183378 -102.275110
v10 5.563110 92.699863
v11 2.699909 95.168114
v12 2.700976 103.385120
v13 2.281731 84.349178
v14 9.719907 94.381715
v15 5.149976 -119.308730
v16 15.692738 -57.591025
v17 10.020727 70.734148
v18 12.269643 -67.106998
v19 5.029569 -61.518344
v20 5.563110 92.699863
v21 7.926685 -18.560431
v22 10.000000 0.000000
v23 12.247990 -72.779714
v24 10.615913 -41.644709
v25 10.615913 -41.644709
v26 6.594170 -63.890173
v27 12.247990 -72.779714
v28 5.563110 92.699863
I_V1 4.873462 -98.660056
I_V2 1.940961 -82.858298
I_V3 4.719081 94.525274
I_V4 5.842672 -86.521779
I_V5 6.490055 -83.573802
I_V6 3.704717 80.775839
I_V7 1.266856 -132.840858
I_V8 1.140866 -95.650822
I_F1 3.881923 -82.858298
I_Ea1 1.029995 60.691270
I_H1 4.026860 71.937257
I_L1 3.651246 -84.027986
I_L2 1.589691 -149.132274
I_L3 1.029995 -119.308730
I_L4 1.609380 -11.044380
I_L5 3.881923 97.141702
I_L6 0.888344 -156.737432
I_F2 3.881923 -82.858298
I_Ea2 1.609380 168.955620
I_H2 1.093990 -10.267379The results from LTSpice are shown below and agree with the Python results.
--- AC Analysis ---
frequency: 0.159155 Hz
V(16): mag: 15.6927 phase: -57.591° voltage
V(8): mag: 3.73418 phase: -63.8026° voltage
V(1): mag: 0 phase: 0° voltage
V(2): mag: 1.26906 phase: -156.737° voltage
V(11): mag: 2.69991 phase: 95.1681° voltage
V(10): mag: 5.56311 phase: 92.6999° voltage
V(23): mag: 12.248 phase: -72.7797° voltage
V(22): mag: 10 phase: 0° voltage
V(9): mag: 2.18338 phase: -102.275° voltage
V(24): mag: 10.6159 phase: -41.6447° voltage
V(3): mag: 5.56311 phase: 92.6999° voltage
V(20): mag: 5.56311 phase: 92.6999° voltage
V(5): mag: 5.04951 phase: -83.1613° voltage
V(12): mag: 2.70098 phase: 103.385° voltage
V(18): mag: 12.2696 phase: -67.107° voltage
V(26): mag: 6.59417 phase: -63.8902° voltage
V(25): mag: 10.6159 phase: -41.6447° voltage
V(4): mag: 5.82288 phase: -82.8583° voltage
V(14): mag: 9.71991 phase: 94.3817° voltage
V(7): mag: 3.88192 phase: 7.1417° voltage
V(15): mag: 5.14998 phase: -119.309° voltage
V(21): mag: 7.92669 phase: -18.5604° voltage
V(13): mag: 2.28173 phase: 84.3492° voltage
V(28): mag: 5.56311 phase: 92.6999° voltage
V(27): mag: 12.248 phase: -72.7797° voltage
V(17): mag: 10.0207 phase: 70.7341° voltage
V(6): mag: 0 phase: 0° voltage
V(19): mag: 5.02957 phase: -61.5183° voltage
I(C1): mag: 2.42683 phase: -70.9646° device_current
I(C2): mag: 0.773901 phase: -80.8809° device_current
I(F1): mag: 3.88192 phase: -82.8583° device_current
I(F2): mag: 3.88192 phase: -82.8583° device_current
I(H1): mag: 4.02686 phase: 71.9373° device_current
I(H2): mag: 1.09399 phase: -10.2674° device_current
I(L1): mag: 3.65125 phase: -84.028° device_current
I(L2): mag: 1.58969 phase: -149.132° device_current
I(L3): mag: 1.03 phase: -119.309° device_current
I(L4): mag: 1.60938 phase: -11.0444° device_current
I(L5): mag: 3.88192 phase: 97.1417° device_current
I(L6): mag: 0.888344 phase: -156.737° device_current
I(I1): mag: 0 phase: 0° device_current
I(I2): mag: 0 phase: 0° device_current
I(I3): mag: 0 phase: 0° device_current
I(I4): mag: 0 phase: 0° device_current
I(R1): mag: 2.39746 phase: -55.6595° device_current
I(R2): mag: 1.86709 phase: -63.8026° device_current
I(R6): mag: 0.253813 phase: -156.737° device_current
I(R8): mag: 0.358508 phase: -89.6236° device_current
I(R10): mag: 1.4803 phase: -118.583° device_current
I(R11): mag: 0.609557 phase: 150.054° device_current
I(R12): mag: 0.634531 phase: -156.737° device_current
I(R14): mag: 0.769305 phase: 88.4942° device_current
I(R15): mag: 1.26686 phase: 47.1591° device_current
I(R7): mag: 0.773901 phase: 99.1191° device_current
I(R16): mag: 0.927185 phase: 92.6999° device_current
I(R3): mag: 0.515704 phase: 167.307° device_current
I(R4): mag: 3.79248 phase: -85.0285° device_current
I(R9): mag: 4.44783 phase: 83.1593° device_current
I(R13): mag: 1.03 phase: -119.309° device_current
I(R17): mag: 1.40714 phase: -72.0029° device_current
I(R18): mag: 1.14087 phase: 84.3492° device_current
I(R19): mag: 1.05441 phase: -80.4269° device_current
I(R20): mag: 2.06528 phase: 104.93° device_current
I(R21): mag: 2.42683 phase: 109.035° device_current
I(R22): mag: 2.49454 phase: 97.4264° device_current
I(R23): mag: 0.773901 phase: 99.1191° device_current
I(R24): mag: 1.38747 phase: -83.3702° device_current
I(R25): mag: 1.76885 phase: -77.3024° device_current
I(R5): mag: 1.85437 phase: 92.6999° device_current
I(G1): mag: 1.84371 phase: -22.7819° device_current
I(G2): mag: 10.099 phase: 96.8387° device_current
I(E1): mag: 1.03 phase: 60.6913° device_current
I(E2): mag: 1.60938 phase: 168.956° device_current
I(V1): mag: 4.87346 phase: -98.6601° device_current
I(V2): mag: 1.94096 phase: -82.8583° device_current
I(V3): mag: 4.71908 phase: 94.5253° device_current
I(V4): mag: 5.84267 phase: -86.5218° device_current
I(V5): mag: 6.49005 phase: -83.5738° device_current
I(V6): mag: 3.70472 phase: 80.7758° device_current
I(V7): mag: 1.26686 phase: -132.841° device_current
I(V8): mag: 1.14087 phase: -95.6508° device_current37.5.2 AC Sweep
Looking at node 17 voltage and comparing the results with those obtained from LTSpice. The frequency sweep is from 0.01 Hz to 1 Hz.
NE = NE_sym.subs(element_values)Display the equations with numeric values.
temp = ''
for i in range(shape(NE.lhs)[0]):
temp += '${:s} = {:s}$<br>'.format(latex(NE.rhs[i]),latex(NE.lhs[i]))
Markdown(temp)\(0 = I_{V2} + 1.0 v_{1} - 0.5 v_{2} - 0.5 v_{8}\)
\(0 = - I_{L6} - 0.5 v_{1} + 0.7 v_{2}\)
\(0 = - I_{V3} + 0.5 v_{3} - 0.333333333333333 v_{4}\)
\(0 = I_{H1} + 2.0 v_{12} - 2.0 v_{13} - 0.333333333333333 v_{3} + 1.33333333333333 v_{4} - 1.0 v_{5}\)
\(0 = - 0.1 v_{12} - 1.0 v_{4} + 1.1 v_{5}\)
\(0 = - I_{V8} - 0.5 v_{13} + 0.5 v_{6}\)
\(0 = - I_{F1} - I_{L5}\)
\(0 = - 0.5 v_{1} - 0.2 v_{16} + 0.95 v_{8} - 0.25 v_{9}\)
\(0 = - I_{L2} + I_{L6} - 0.1 v_{10} - 0.25 v_{8} + 0.35 v_{9}\)
\(0 = I_{V3} + I_{V4} + 0.225 v_{10} - 0.125 v_{11} - 0.1 v_{9}\)
\(0 = - I_{L4} - 0.125 v_{10} + v_{11} \cdot \left(2.0 s + 0.125\right) + v_{12} \left(- 2.0 s - 2.0\right) + 2.0 v_{13}\)
\(0 = - 2.0 s v_{11} + v_{12} \cdot \left(2.0 s + 0.1\right) - 0.1 v_{5}\)
\(0 = 1.03333333333333 v_{13} - 0.333333333333333 v_{14} - 0.2 v_{19} - 0.5 v_{6}\)
\(0 = I_{F1} - 0.333333333333333 v_{13} + 0.666666666666667 v_{14} - 0.333333333333333 v_{20}\)
\(0 = I_{Ea1} + 0.2 v_{15}\)
\(0 = I_{L1} + 0.533333333333333 v_{16} - 0.333333333333333 v_{22} - 2.0 v_{5} - 0.2 v_{8}\)
\(0 = I_{Ea2} + I_{L4}\)
\(0 = - 2.0 s v_{23} + v_{18} \cdot \left(2.0 s + 0.333333333333333\right) - 0.333333333333333 v_{19}\)
\(0 = - 0.2 v_{13} - 0.333333333333333 v_{18} + 0.876190476190476 v_{19} - 0.2 v_{20} - 0.142857142857143 v_{23}\)
\(0 = - I_{V4} + I_{V5} - 0.333333333333333 v_{14} - 0.2 v_{19} + 0.533333333333333 v_{20}\)
\(0 = - I_{Ea1} - I_{L3}\)
\(0 = I_{L3} + I_{V1} - 0.333333333333333 v_{16} + 0.444444444444444 v_{22} - 0.111111111111111 v_{23}\)
\(0 = - I_{L1} + I_{V6} - 2.0 s v_{18} - 0.142857142857143 v_{19} - 0.111111111111111 v_{22} + v_{23} \cdot \left(2.0 s + 0.553968253968254\right) - 0.2 v_{24} - 0.1 v_{28}\)
\(0 = I_{V7} - 0.2 v_{23} + 0.2 v_{24}\)
\(0 = I_{L2} - I_{V7} + 0.1 v_{25} - 0.1 v_{26}\)
\(0 = - I_{Ea2} - I_{H2} - 0.1 v_{25} + 0.1 v_{26}\)
\(0 = - I_{F2} + I_{H2} - I_{V6}\)
\(0 = - I_{V5} - 0.1 v_{23} + 0.433333333333333 v_{28} + 2.0 v_{5}\)
\(10.0 = v_{22}\)
\(0 = v_{1}\)
\(0 = v_{10} - v_{3}\)
\(0 = v_{10} - v_{20}\)
\(0 = v_{20} - v_{28}\)
\(0 = v_{23} - v_{27}\)
\(0 = v_{24} - v_{25}\)
\(0 = - v_{6}\)
\(0 = I_{F1} - 2.0 I_{V2}\)
\(0 = v_{15} - 2.0 v_{2} - v_{21} + 2.0 v_{7}\)
\(0 = - 3.0 I_{V2} + v_{4}\)
\(0 = - 1.0 I_{L1} s - 1.414 I_{L2} s + v_{16} - v_{23}\)
\(0 = - 1.414 I_{L1} s - 4.0 I_{L2} s + v_{25} - v_{9}\)
\(0 = - 2.0 I_{L3} s - 2.23573030573904 I_{L4} s - v_{21} + v_{22}\)
\(0 = - 2.23573030573904 I_{L3} s - 5.0 I_{L4} s - v_{11} + v_{17}\)
\(0 = - 1.0 I_{L5} s - v_{7}\)
\(0 = - 2.0 I_{L6} s - v_{2} + v_{9}\)
\(0 = I_{F2} - 2.0 I_{V2}\)
\(0 = - 2.0 v_{10} + v_{17} - v_{26} + 2.0 v_{9}\)
\(0 = - 3.0 I_{V2} - v_{26} + v_{27}\)
Solve for voltages and currents.
U_ac = solve(NE,X)37.5.3 Plot the voltage at node 10
H = U_ac[v17]num, denom = fraction(H) #returns numerator and denominator
# convert symbolic to numpy polynomial
a = np.array(Poly(num, s).all_coeffs(), dtype=float)
b = np.array(Poly(denom, s).all_coeffs(), dtype=float)
system = (a, b)#x = np.linspace(0.01*2*np.pi, 1*2*np.pi, 200, endpoint=True)
x = np.logspace(-2, 0, 1000, endpoint=False)*2*np.pi
w, mag, phase = signal.bode(system, w=x) # returns: rad/s, mag in dB, phase in degLoad the csv file of node 10 voltage over the sweep range and plot along with the results obtained from SymPy.
fn = 'test_7.csv' # data from LTSpice
LTSpice_data = np.genfromtxt(fn, delimiter=',')# initaliaze some empty arrays
frequency = np.zeros(len(LTSpice_data))
voltage = np.zeros(len(LTSpice_data)).astype(complex)
# convert the csv data to complez numbers and store in the array
for i in range(len(LTSpice_data)):
frequency[i] = LTSpice_data[i][0]
voltage[i] = LTSpice_data[i][1] + LTSpice_data[i][2]*1jPlot the results.
Using
np.unwrap(2 * phase) / 2)
to keep the pahse plots the same.
fig, ax1 = plt.subplots()
ax1.set_ylabel('magnitude, dB')
ax1.set_xlabel('frequency, Hz')
plt.semilogx(frequency, 20*np.log10(np.abs(voltage)),'-r') # Bode magnitude plot
plt.semilogx(w/(2*np.pi), mag,'-b') # Bode magnitude plot
ax1.tick_params(axis='y')
#ax1.set_ylim((-30,20))
plt.grid()
# instantiate a second y-axes that shares the same x-axis
ax2 = ax1.twinx()
color = 'tab:blue'
plt.semilogx(frequency, np.unwrap(2*np.angle(voltage)/2) *180/np.pi,':',color=color) # Bode phase plot
plt.semilogx(w/(2*np.pi), phase,':',color='tab:red') # Bode phase plot
ax2.set_ylabel('phase, deg',color=color)
ax2.tick_params(axis='y', labelcolor=color)
#ax2.set_ylim((-5,25))
plt.title('Magnitude and phase response')
plt.show()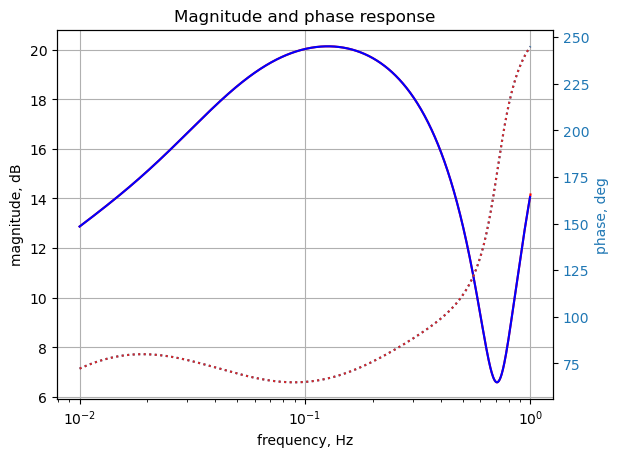
fig, ax1 = plt.subplots()
ax1.set_ylabel('magnitude difference')
ax1.set_xlabel('frequency, Hz')
plt.semilogx(frequency[0:-1], np.abs(voltage[0:-1])-10**(mag/20),'-r') # Bode magnitude plot
#plt.semilogx(w/(2*np.pi), mag,'-b') # Bode magnitude plot
ax1.tick_params(axis='y')
#ax1.set_ylim((-30,20))
plt.grid()
# instantiate a second y-axes that shares the same x-axis
ax2 = ax1.twinx()
color = 'tab:blue'
plt.semilogx(frequency[0:-1], np.unwrap(2*np.angle(voltage[0:-1])/2) *180/np.pi - phase,':',color=color) # Bode phase plot
#plt.semilogx(w/(2*np.pi), phase,':',color='tab:red') # Bode phase plot
ax2.set_ylabel('phase difference, deg',color=color)
ax2.tick_params(axis='y', labelcolor=color)
#ax2.set_ylim((-5,25))
plt.title('Difference between LTSpice and Python results')
plt.show()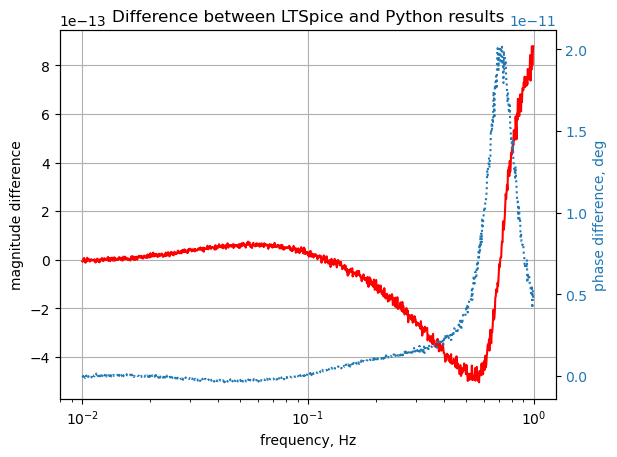
The SymPy and LTSpice results overlay each other. The scale for the magnitude is \(10^{-13}\) and \(10^{-11}\) for the phase indicating the numerical difference is very small.