5  Resistive Networks

This chapter focuses on the analysis of electric circuits containing independed sources, dependent sources and resistors. The simplest and most common circuit element is the resistor. Many principles of circuit analysis can be explored by considereing circuits that only have components that don’t store energy and are frequency independent.

The study and analysis of resistive circuits can serve as an introduction to the essential framework for understanding how energy is distributed and controlled in nearly every electronic device by applying Ohm’s Law and Kirchhoff’s Laws to predict how electric current will flow in resistive circuits. For circuits having many nodes or branches, modified nodal analysis is an algorithmic method which can be used to obtain network equations for almost any electric circuit.

from sympy import *
import numpy as np
from tabulate import tabulate
from scipy import signal
import matplotlib.pyplot as plt
import pandas as pd
import SymMNA
from IPython.display import display, Markdown, Math, Latex
init_printing()
import re

This chapter examines several resistive circuits, each selected to illustrate different facets of circuit analysis and the corresponding techniques required to solve them. These examples illustrate the variety of complexity encountered in circuit theory, ranging from problems easily handled by manual calculation to those necessitating algorithmic, computer-aided methods.

Example	Description
Circuit 1	Five resistors, two independent sources and four nodes.
Circuit 2	Nonplanar topology with 12 resistors, 3 independent voltage sources (2 set to zero for measurement), 1 independent current source, and 4 dependent sources.
Circuit 3	A circuit having 45 branches, 22 nodes and 44 resistors.

5.1 Circuit Example 1

The circuit shown in the schematic below has five reisistors and two indpendent sources, \(V_1\) and \(I_1\). The schematics was drawn using LTSpice and the netlist was copied by using the View/SPICE netlist command.

The circuit has four nodes and a solution by pencil and paper is doable on a circuit of this size. The system of equations obtained by either node or loop analysis could be solved by hand or on a scientific calculator. Solutions to the network equations are shown in the example.

The circuit is notable in that neither \(V_1\) or \(I_1\) are connected to the reference node. If loop equations are written for the circuit, two equations can describe the operation of the circuit. If node equations are written, four equations are required and \(V_1\) will form a supernode between nodes 3 and 4. As show below, the MNA method will generate five equations. The increase in number of equations is the price paid for using an algorithmic method that can be implemented in computer code.

Figure 5.1: Schematic for example 1.

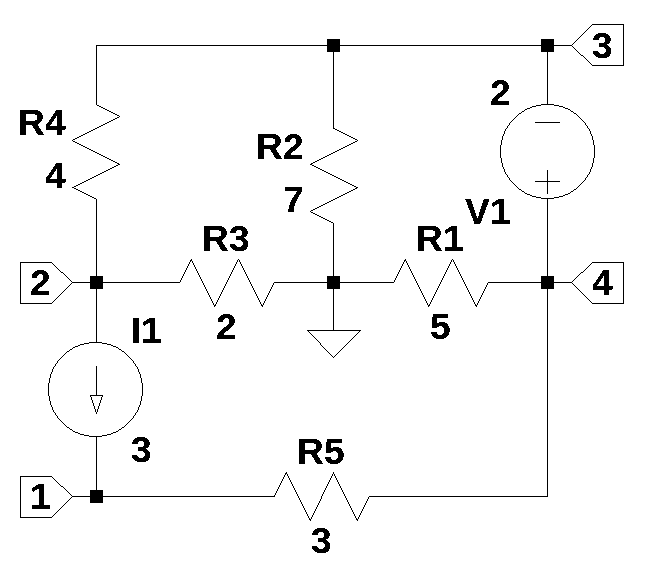
The circuit shown above is can be analyzed by hand with pencil and paper and is the type of problem students would encounter in an engineering circuit analysis classes.

5.1.0.1 Python MNA Solution

The schematic above was drawn using LTSpice and the netlist was obtained and copied below. The nodes were numbered in no particular order, except to keep \(V_1\) away from the reference node.

Load the net list of Figure 5.1.

net_list = '''
R1 0 4 5
R2 0 3 7
R3 0 2 2
R4 2 3 4
V1 4 3 2
I1 2 1 3
R5 1 4 3
'''

Call the symbolic modified nodal analysis function, SymMNA.smna(net_list). The internals of this function were explained in Chapter 4. Several parameters are returned by the function, but only the matrices \(A\), \(X\) and \(Z\) are used in the analysis below.

report, network_df, i_unk_df, A, X, Z = SymMNA.smna(net_list)

The \(A\) matrix is shown below. As describe in the introduction, it is compised of the \(G\), \(B\), \(C\) and \(M\) matricies.

\(\displaystyle \left[\begin{matrix}\frac{1}{R_{5}} & 0 & 0 & - \frac{1}{R_{5}} & 0\\0 & \frac{1}{R_{4}} + \frac{1}{R_{3}} & - \frac{1}{R_{4}} & 0 & 0\\0 & - \frac{1}{R_{4}} & \frac{1}{R_{4}} + \frac{1}{R_{2}} & 0 & -1\\- \frac{1}{R_{5}} & 0 & 0 & \frac{1}{R_{5}} + \frac{1}{R_{1}} & 1\\0 & 0 & -1 & 1 & 0\end{matrix}\right]\)

The \(X\) matrix contains the symbols for the unknown node voltages and the current from \(V_1\).

\(\displaystyle \left[ v_{1}, \ v_{2}, \ v_{3}, \ v_{4}, \ I_{V1}\right]\)

The \(Z\) matrix contains the symbols for the left side of the newtork equations.

\(\displaystyle \left[ I_{1}, \ - I_{1}, \ 0, \ 0, \ V_{1}\right]\)

The code below assembles the network equations from the MNA matrices and displays the equations.

# Put matrices into SymPy 
X = Matrix(X)
Z = Matrix(Z)

NE_sym = Eq(A*X,Z)

# display the equations
temp = ''
for i in range(shape(NE_sym.lhs)[0]):
    temp += '${:s} = {:s}$<br>'.format(latex(NE_sym.rhs[i]),latex(NE_sym.lhs[i]))
Markdown(temp)

\(I_{1} = \frac{v_{1}}{R_{5}} - \frac{v_{4}}{R_{5}}\)
\(- I_{1} = v_{2} \cdot \left(\frac{1}{R_{4}} + \frac{1}{R_{3}}\right) - \frac{v_{3}}{R_{4}}\)
\(0 = - I_{V1} + v_{3} \cdot \left(\frac{1}{R_{4}} + \frac{1}{R_{2}}\right) - \frac{v_{2}}{R_{4}}\)
\(0 = I_{V1} + v_{4} \cdot \left(\frac{1}{R_{5}} + \frac{1}{R_{1}}\right) - \frac{v_{1}}{R_{5}}\)
\(V_{1} = - v_{3} + v_{4}\)

The free symbols are entered as SymPy variables and the element values are put into a dictionary.

var(str(NE_sym.free_symbols).replace('{','').replace('}',''))
element_values = SymMNA.get_part_values(network_df) # get element vales from netlist

The network equations for the netlist can be solved symbolically and the node voltages and dependent currents are displayed using symbolic notation.

U_sym = solve(NE_sym,X)

Display the symbolic solution

temp = ''
for i in U_sym.keys():
    temp += '${:s} = {:s}$<br>'.format(latex(i),latex(U_sym[i]))

Markdown(temp)

\(v_{1} = \frac{I_{1} R_{1} R_{2} R_{4} + I_{1} R_{1} R_{2} R_{5} + I_{1} R_{1} R_{3} R_{5} + I_{1} R_{1} R_{4} R_{5} + I_{1} R_{2} R_{3} R_{5} + I_{1} R_{2} R_{4} R_{5} + R_{1} R_{2} V_{1} + R_{1} R_{3} V_{1} + R_{1} R_{4} V_{1}}{R_{1} R_{2} + R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}\)
\(v_{2} = \frac{- I_{1} R_{1} R_{3} R_{4} - I_{1} R_{2} R_{3} R_{4} - R_{2} R_{3} V_{1}}{R_{1} R_{2} + R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}\)
\(v_{3} = \frac{I_{1} R_{1} R_{2} R_{4} - R_{2} R_{3} V_{1} - R_{2} R_{4} V_{1}}{R_{1} R_{2} + R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}\)
\(v_{4} = \frac{I_{1} R_{1} R_{2} R_{4} + R_{1} R_{2} V_{1} + R_{1} R_{3} V_{1} + R_{1} R_{4} V_{1}}{R_{1} R_{2} + R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}\)
\(I_{V1} = \frac{I_{1} R_{1} R_{2} + I_{1} R_{1} R_{3} + I_{1} R_{1} R_{4} + I_{1} R_{2} R_{3} - R_{2} V_{1} - R_{3} V_{1} - R_{4} V_{1}}{R_{1} R_{2} + R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}\)

Find the numerical solution for the node voltages by substituting the element values into the network equation and display the equations.

NE = NE_sym.subs(element_values)

temp = ''
for i in range(shape(NE.lhs)[0]):
    temp += '${:s} = {:s}$<br>'.format(latex(NE.rhs[i]),latex(NE.lhs[i]))

Markdown(temp)

\(3.0 = 0.333333333333333 v_{1} - 0.333333333333333 v_{4}\)
\(-3.0 = 0.75 v_{2} - 0.25 v_{3}\)
\(0 = - I_{V1} - 0.25 v_{2} + 0.392857142857143 v_{3}\)
\(0 = I_{V1} - 0.333333333333333 v_{1} + 0.533333333333333 v_{4}\)
\(2.0 = - v_{3} + v_{4}\)

Solve for voltages and currents.

U = solve(NE,X)

Display the numerical solution using six digits to the right of the decimal so that results can be compared to the solution obtained from LTSpice.

table_header = ['unknowns', 'values','units']
table_row = []

for name, value in U.items():
    if str(name)[0] == 'I':
        unit = 'device current'
    else:
        unit = 'voltage'
    table_row.append([str(name),float(value),str(unit)])

print(tabulate(table_row, headers=table_header,colalign = ('right','decimal','left'),
    tablefmt="simple",floatfmt=('5s','.6f','20s')))

  unknowns     values  units
----------  ---------  --------------
        v1  14.140187  voltage
        v2  -2.953271  voltage
        v3   3.140187  voltage
        v4   5.140187  voltage
      I_V1   1.971963  device current

The Sympy generated solution matches the LTSpice results:

V(1):    14.1402     voltage
V(2):    -2.95327    voltage
V(3):    3.14019     voltage
V(4):    5.14019     voltage
I(V1):   1.97196     device_current

5.2 Example Circuit 2

The circuit shown in the schematic below is a nonplanar assembly of resistors, independent and dependent sources. The circuit can be visualized as a cube. The nodes 1, 2, 0, 9, 4, 5, 6, and 7 form the corners of a cube and the compoenets in the circuit are the edges of the cube. The junction of \(R_2\), \(R_{11}\) and \(R_3\) was arbitrailary chosen as the reference node.

The circuit has 12 resistors, 3 independent voltage sources, two of which are set to zero inorder to measure the current through the branch. There is one independent current source and there are 4 dependent sources, one of each type. It would be rather difficult and tedious to derive the network equations for this circuit by manual procedures employing either traditional nodal or loop analysis. In this example, the MNA procedure with SymPy can easily generate network equations and symbolically solve for the node voltages. As shown below the symbolic expressions can be very long and do not provide much insight into the circuit’s behavor.

Figure 5.2: Schematic for exapmple 2.

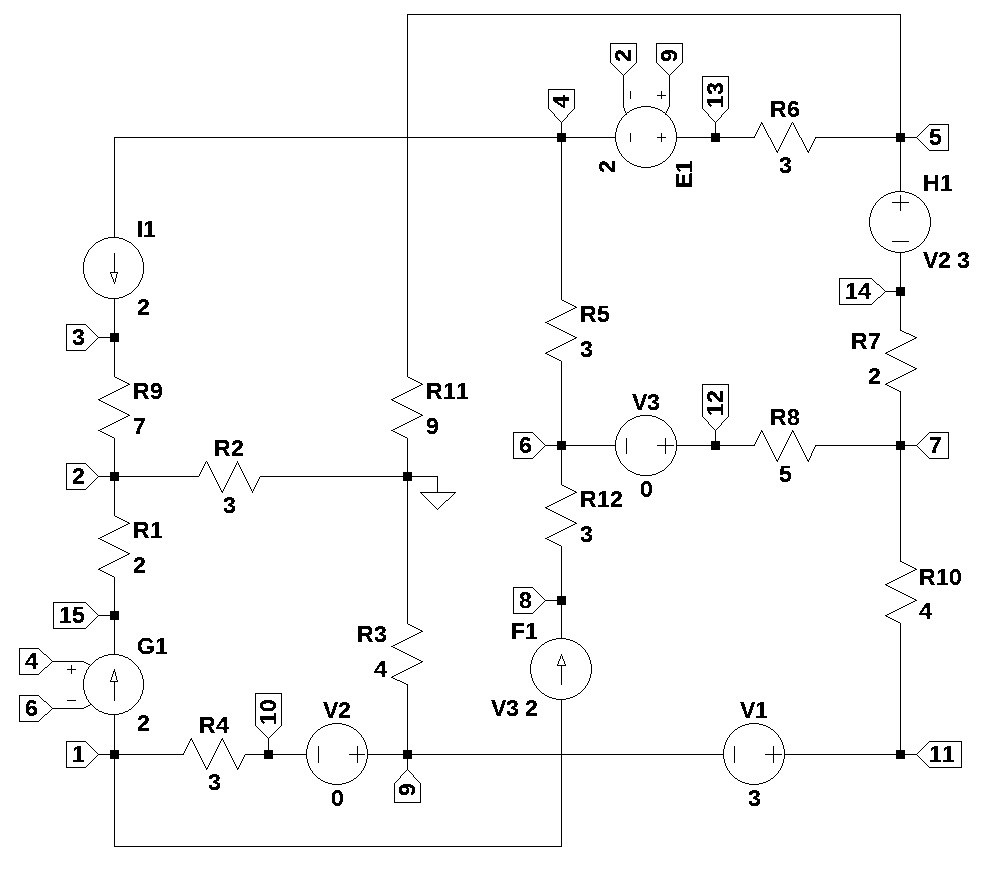
Additionally, the most efficient way to generate netlists is from a schematic capture program. If the schematic is drawn corretly, the netlist will be correct.

Load the net list

net_list = '''
R1 2 15 2
R2 0 2 3
R3 9 0 4
R4 1 10 3
R5 4 6 3
R6 5 13 3
R7 7 14 2
R8 12 7 5
R9 3 2 7
R10 7 11 4
R11 5 0 9
R12 6 8 3
I1 4 3 2
V1 11 9 3
E1 13 4 9 2 2
F1 1 8 V3 2
G1 1 15 4 7 3
H1 5 14 V2 3
V2 9 10 0
V3 12 6 0
'''

Call the symbolic modified nodal analysis function.

report, network_df, i_unk_df, A, X, Z = SymMNA.smna(net_list)

Build and display the network equations.

# Put matrices into SymPy 
X = Matrix(X)
Z = Matrix(Z)

NE_sym = Eq(A*X,Z)

# turn the free symbols into SymPy variables.
var(str(NE_sym.free_symbols).replace('{','').replace('}',''))

# construct a dictionary of element values
element_values = SymMNA.get_part_values(network_df)

temp = ''
for i in range(len(X)):
    temp += '${:s}$<br>'.format(latex(Eq((A*X)[i:i+1][0],Z[i])))

Markdown(temp)

\(I_{F1} + g_{1} v_{4} - g_{1} v_{7} + \frac{v_{1}}{R_{4}} - \frac{v_{10}}{R_{4}} = 0\)
\(v_{2} \cdot \left(\frac{1}{R_{9}} + \frac{1}{R_{2}} + \frac{1}{R_{1}}\right) - \frac{v_{3}}{R_{9}} - \frac{v_{15}}{R_{1}} = 0\)
\(- \frac{v_{2}}{R_{9}} + \frac{v_{3}}{R_{9}} = I_{1}\)
\(- I_{Ea1} + \frac{v_{4}}{R_{5}} - \frac{v_{6}}{R_{5}} = - I_{1}\)
\(I_{H1} + v_{5} \cdot \left(\frac{1}{R_{6}} + \frac{1}{R_{11}}\right) - \frac{v_{13}}{R_{6}} = 0\)
\(- I_{V3} + v_{6} \cdot \left(\frac{1}{R_{5}} + \frac{1}{R_{12}}\right) - \frac{v_{4}}{R_{5}} - \frac{v_{8}}{R_{12}} = 0\)
\(v_{7} \cdot \left(\frac{1}{R_{8}} + \frac{1}{R_{7}} + \frac{1}{R_{10}}\right) - \frac{v_{12}}{R_{8}} - \frac{v_{14}}{R_{7}} - \frac{v_{11}}{R_{10}} = 0\)
\(- I_{F1} - \frac{v_{6}}{R_{12}} + \frac{v_{8}}{R_{12}} = 0\)
\(- I_{V1} + I_{V2} + \frac{v_{9}}{R_{3}} = 0\)
\(- I_{V2} - \frac{v_{1}}{R_{4}} + \frac{v_{10}}{R_{4}} = 0\)
\(I_{V1} + \frac{v_{11}}{R_{10}} - \frac{v_{7}}{R_{10}} = 0\)
\(I_{V3} + \frac{v_{12}}{R_{8}} - \frac{v_{7}}{R_{8}} = 0\)
\(I_{Ea1} + \frac{v_{13}}{R_{6}} - \frac{v_{5}}{R_{6}} = 0\)
\(- I_{H1} + \frac{v_{14}}{R_{7}} - \frac{v_{7}}{R_{7}} = 0\)
\(- g_{1} v_{4} + g_{1} v_{7} + \frac{v_{15}}{R_{1}} - \frac{v_{2}}{R_{1}} = 0\)
\(v_{11} - v_{9} = V_{1}\)
\(- v_{10} + v_{9} = V_{2}\)
\(v_{12} - v_{6} = V_{3}\)
\(ea_{1} v_{2} - ea_{1} v_{9} + v_{13} - v_{4} = 0\)
\(I_{F1} - I_{V3} f_{1} = 0\)
\(- I_{V2} h_{1} - v_{14} + v_{5} = 0\)

While manual circuit analysis is a fundamental skill, certain network topologies reach a level of complexity where traditional “pencil and paper” methods become impractical. The circuit shown in Figure 5.2 serves as an example of such a system. When dealing with multi-loop circuits containing numerous passive components and dependent sources, the resulting system of linear equations grows significantly. Analyzing this specific circuit by hand would be prone to human error. To overcome these hurdles, we can use SymPy. SymPy allows us to define circuit parameters as symbols, set up the MNA equations and solve the system algebraically. What might take a human hours of frustration can be processed by a computer in seconds or minutes.

To quantify this efficiency, we can utilize the IPython magic command %%time. When placed at the very top of a code cell, it tracks the CPU and wall-clock time required to execute the entire block. Find the symbolic solution and time how long it takes.

%%time
U_sym = solve(NE_sym,X)

CPU times: user 57.2 s, sys: 4.76 ms, total: 57.2 s
Wall time: 57.3 s

CPU time refers to the amount of time the CPU spends processing instructions of a program. It specifically measures the time during which the CPU is actively working on executing a task, excluding time spent waiting for input/output operations or when the program is idle. Wall time refers to the total elapsed real-world time taken to execute the code cell. Unlike CPU time, which measures active processing time by the CPU alone, wall time accounts for all the time from the start to the end of a task as experienced by the user. The times displayed above were obtained on an Intel i3-4160 CPU @ 3.60GHz.

The follwoing code will display the symbolic solutions for the unknown network variables.

temp = ''
for i in U_sym.keys():
    temp += '${:s} = {:s}$<br>'.format(latex(i),latex(U_sym[i]))

Markdown(temp)

\(v_{1} = \frac{I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{10} R_{2} R_{4} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{4} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{4} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{4} ea_{1} f_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{10} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{10} R_{3} R_{6} f_{1} - I_{1} R_{10} R_{4} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{10} R_{4} R_{5} R_{6} g_{1} - I_{1} R_{10} R_{4} R_{6} R_{8} g_{1} + I_{1} R_{10} R_{4} R_{6} f_{1} + I_{1} R_{11} R_{2} R_{4} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{4} R_{5} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{4} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{4} ea_{1} f_{1} + I_{1} R_{11} R_{3} R_{4} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{11} R_{3} R_{4} R_{5} ea_{1} g_{1} + I_{1} R_{11} R_{3} R_{4} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{4} ea_{1} f_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} - I_{1} R_{11} R_{4} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{4} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{4} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{4} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{4} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{4} R_{6} f_{1} - I_{1} R_{11} R_{4} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{4} R_{7} f_{1} + I_{1} R_{2} R_{3} R_{4} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{4} R_{5} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{4} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{4} ea_{1} f_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} + I_{1} R_{2} R_{4} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{4} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{4} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{4} R_{7} ea_{1} f_{1} - I_{1} R_{3} R_{4} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{3} R_{4} R_{5} R_{6} g_{1} - I_{1} R_{3} R_{4} R_{6} R_{8} g_{1} + I_{1} R_{3} R_{4} R_{6} f_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} - I_{1} R_{4} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{4} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{4} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{4} R_{6} R_{7} f_{1} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{4} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{5} V_{2} ea_{1} g_{1} - R_{10} R_{2} R_{8} V_{2} ea_{1} g_{1} - R_{10} R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{10} R_{3} R_{5} V_{2} ea_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} g_{1} - R_{10} R_{3} R_{7} V_{3} g_{1} - R_{10} R_{3} R_{8} V_{2} ea_{1} g_{1} + R_{10} R_{3} V_{2} ea_{1} f_{1} - R_{10} R_{3} V_{3} f_{1} - R_{10} R_{4} R_{6} V_{3} f_{1} g_{1} - R_{10} R_{4} R_{6} V_{3} g_{1} - R_{10} R_{4} R_{7} V_{3} g_{1} - R_{10} R_{4} V_{3} f_{1} - R_{10} R_{5} V_{2} f_{1} g_{1} h_{1} + R_{10} R_{5} V_{2} f_{1} - R_{10} R_{5} V_{2} g_{1} h_{1} + R_{10} R_{5} V_{2} + R_{10} R_{6} V_{2} f_{1} + R_{10} R_{6} V_{2} + R_{10} R_{7} V_{2} - R_{10} R_{8} V_{2} g_{1} h_{1} + R_{10} R_{8} V_{2} + R_{10} V_{2} f_{1} h_{1} + R_{11} R_{2} R_{4} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{5} V_{2} ea_{1} g_{1} - R_{11} R_{2} R_{8} V_{2} ea_{1} g_{1} + R_{11} R_{3} R_{4} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{5} V_{2} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} - R_{11} R_{3} R_{8} V_{2} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} - R_{11} R_{4} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{4} R_{6} V_{3} g_{1} - R_{11} R_{4} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{4} R_{7} V_{3} g_{1} - R_{11} R_{4} V_{3} f_{1} - R_{11} R_{5} V_{2} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{2} f_{1} - R_{11} R_{5} V_{2} g_{1} h_{1} + R_{11} R_{5} V_{2} + R_{11} R_{6} V_{2} f_{1} + R_{11} R_{6} V_{2} + R_{11} R_{7} V_{2} f_{1} + R_{11} R_{7} V_{2} - R_{11} R_{8} V_{2} g_{1} h_{1} + R_{11} R_{8} V_{2} + R_{11} V_{2} f_{1} h_{1} + R_{2} R_{3} R_{4} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{2} R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{2} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{2} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{2} R_{3} R_{8} V_{2} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{4} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{5} R_{7} V_{2} ea_{1} f_{1} g_{1} - R_{2} R_{5} R_{7} V_{2} ea_{1} g_{1} - R_{2} R_{7} R_{8} V_{2} ea_{1} g_{1} + R_{3} R_{4} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{4} R_{5} V_{1} ea_{1} g_{1} - R_{3} R_{4} R_{6} V_{3} f_{1} g_{1} - R_{3} R_{4} R_{6} V_{3} g_{1} - R_{3} R_{4} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{4} R_{7} V_{3} g_{1} + R_{3} R_{4} R_{8} V_{1} ea_{1} g_{1} - R_{3} R_{4} V_{1} ea_{1} f_{1} - R_{3} R_{4} V_{3} f_{1} - R_{3} R_{5} R_{7} V_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} ea_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} g_{1} - R_{3} R_{5} V_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} f_{1} - R_{3} R_{5} V_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} - R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{2} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{2} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{2} f_{1} - R_{3} R_{5} V_{2} g_{1} h_{1} + R_{3} R_{5} V_{2} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} + R_{3} R_{6} V_{1} f_{1} + R_{3} R_{6} V_{1} + R_{3} R_{6} V_{2} f_{1} + R_{3} R_{6} V_{2} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} - R_{3} R_{7} R_{8} V_{1} g_{1} - R_{3} R_{7} R_{8} V_{2} ea_{1} g_{1} - R_{3} R_{7} R_{8} V_{2} g_{1} + R_{3} R_{7} V_{1} f_{1} + R_{3} R_{7} V_{1} + R_{3} R_{7} V_{2} ea_{1} f_{1} + R_{3} R_{7} V_{2} ea_{1} + R_{3} R_{7} V_{2} f_{1} + R_{3} R_{7} V_{2} - R_{3} R_{7} V_{3} f_{1} - R_{3} R_{7} V_{3} - R_{3} R_{8} V_{1} g_{1} h_{1} + R_{3} R_{8} V_{1} - R_{3} R_{8} V_{2} ea_{1} g_{1} h_{1} - R_{3} R_{8} V_{2} g_{1} h_{1} + R_{3} R_{8} V_{2} + R_{3} V_{1} f_{1} h_{1} + R_{3} V_{2} ea_{1} f_{1} h_{1} + R_{3} V_{2} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1} - R_{4} R_{5} R_{7} V_{1} f_{1} g_{1} - R_{4} R_{5} R_{7} V_{1} g_{1} - R_{4} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{4} R_{6} R_{7} V_{3} g_{1} - R_{4} R_{7} R_{8} V_{1} g_{1} + R_{4} R_{7} V_{1} f_{1} - R_{4} R_{7} V_{3} f_{1} + R_{5} R_{7} V_{2} f_{1} + R_{5} R_{7} V_{2} + R_{6} R_{7} V_{2} f_{1} + R_{6} R_{7} V_{2} + R_{7} R_{8} V_{2}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{2} = \frac{I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{10} R_{2} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{5} R_{6} g_{1} + I_{1} R_{10} R_{2} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} f_{1} + I_{1} R_{10} R_{2} R_{5} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} + I_{1} R_{10} R_{2} R_{6} R_{8} g_{1} - I_{1} R_{10} R_{2} R_{6} f_{1} - I_{1} R_{10} R_{2} R_{6} - I_{1} R_{10} R_{2} R_{7} + I_{1} R_{10} R_{2} R_{8} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} - I_{1} R_{10} R_{2} f_{1} h_{1} + I_{1} R_{11} R_{2} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{6} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{7} g_{1} + I_{1} R_{11} R_{2} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} f_{1} + I_{1} R_{11} R_{2} R_{5} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} + I_{1} R_{11} R_{2} R_{6} R_{8} g_{1} - I_{1} R_{11} R_{2} R_{6} f_{1} - I_{1} R_{11} R_{2} R_{6} + I_{1} R_{11} R_{2} R_{7} R_{8} g_{1} - I_{1} R_{11} R_{2} R_{7} f_{1} - I_{1} R_{11} R_{2} R_{7} + I_{1} R_{11} R_{2} R_{8} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{8} - I_{1} R_{11} R_{2} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} f_{1} + I_{1} R_{2} R_{3} R_{5} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} + I_{1} R_{2} R_{3} R_{6} R_{8} g_{1} - I_{1} R_{2} R_{3} R_{6} f_{1} - I_{1} R_{2} R_{3} R_{6} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} - I_{1} R_{2} R_{3} R_{7} f_{1} - I_{1} R_{2} R_{3} R_{7} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{8} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{5} R_{6} R_{7} f_{1} g_{1} + I_{1} R_{2} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{2} R_{5} R_{7} f_{1} - I_{1} R_{2} R_{5} R_{7} + I_{1} R_{2} R_{6} R_{7} R_{8} g_{1} - I_{1} R_{2} R_{6} R_{7} f_{1} - I_{1} R_{2} R_{6} R_{7} - I_{1} R_{2} R_{7} R_{8} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{6} V_{3} f_{1} g_{1} + R_{10} R_{2} R_{6} V_{3} g_{1} + R_{10} R_{2} R_{7} V_{3} g_{1} + R_{10} R_{2} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{2} R_{6} V_{3} f_{1} g_{1} + R_{11} R_{2} R_{6} V_{3} g_{1} + R_{11} R_{2} R_{7} V_{3} f_{1} g_{1} + R_{11} R_{2} R_{7} V_{3} g_{1} + R_{11} R_{2} V_{3} f_{1} g_{1} h_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{2} R_{3} R_{6} V_{3} f_{1} g_{1} + R_{2} R_{3} R_{6} V_{3} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} g_{1} - R_{2} R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} g_{1} + R_{2} R_{6} R_{7} V_{3} f_{1} g_{1} + R_{2} R_{6} R_{7} V_{3} g_{1} + R_{2} R_{7} R_{8} V_{1} g_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{3} = \frac{I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{10} R_{2} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{5} R_{6} g_{1} + I_{1} R_{10} R_{2} R_{5} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{5} R_{9} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} f_{1} + I_{1} R_{10} R_{2} R_{5} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} + I_{1} R_{10} R_{2} R_{6} R_{8} g_{1} - I_{1} R_{10} R_{2} R_{6} f_{1} - I_{1} R_{10} R_{2} R_{6} - I_{1} R_{10} R_{2} R_{7} + I_{1} R_{10} R_{2} R_{8} R_{9} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{8} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} - I_{1} R_{10} R_{2} f_{1} h_{1} + I_{1} R_{10} R_{3} R_{5} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{3} R_{5} R_{9} ea_{1} g_{1} + I_{1} R_{10} R_{3} R_{8} R_{9} ea_{1} g_{1} - I_{1} R_{10} R_{3} R_{9} ea_{1} f_{1} + I_{1} R_{10} R_{5} R_{9} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{9} f_{1} + I_{1} R_{10} R_{5} R_{9} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{9} - I_{1} R_{10} R_{6} R_{9} f_{1} - I_{1} R_{10} R_{6} R_{9} - I_{1} R_{10} R_{7} R_{9} + I_{1} R_{10} R_{8} R_{9} g_{1} h_{1} - I_{1} R_{10} R_{8} R_{9} - I_{1} R_{10} R_{9} f_{1} h_{1} + I_{1} R_{11} R_{2} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{6} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{7} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{9} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} f_{1} + I_{1} R_{11} R_{2} R_{5} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} + I_{1} R_{11} R_{2} R_{6} R_{8} g_{1} - I_{1} R_{11} R_{2} R_{6} f_{1} - I_{1} R_{11} R_{2} R_{6} + I_{1} R_{11} R_{2} R_{7} R_{8} g_{1} - I_{1} R_{11} R_{2} R_{7} f_{1} - I_{1} R_{11} R_{2} R_{7} + I_{1} R_{11} R_{2} R_{8} R_{9} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{8} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{8} - I_{1} R_{11} R_{2} f_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{11} R_{3} R_{5} R_{9} ea_{1} g_{1} + I_{1} R_{11} R_{3} R_{8} R_{9} ea_{1} g_{1} + I_{1} R_{11} R_{5} R_{9} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{5} R_{9} f_{1} + I_{1} R_{11} R_{5} R_{9} g_{1} h_{1} - I_{1} R_{11} R_{5} R_{9} - I_{1} R_{11} R_{6} R_{9} f_{1} - I_{1} R_{11} R_{6} R_{9} - I_{1} R_{11} R_{7} R_{9} f_{1} - I_{1} R_{11} R_{7} R_{9} + I_{1} R_{11} R_{8} R_{9} g_{1} h_{1} - I_{1} R_{11} R_{8} R_{9} - I_{1} R_{11} R_{9} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{9} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} f_{1} + I_{1} R_{2} R_{3} R_{5} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} + I_{1} R_{2} R_{3} R_{6} R_{8} g_{1} - I_{1} R_{2} R_{3} R_{6} f_{1} - I_{1} R_{2} R_{3} R_{6} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} - I_{1} R_{2} R_{3} R_{7} f_{1} - I_{1} R_{2} R_{3} R_{7} + I_{1} R_{2} R_{3} R_{8} R_{9} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{8} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{5} R_{6} R_{7} f_{1} g_{1} + I_{1} R_{2} R_{5} R_{6} R_{7} g_{1} + I_{1} R_{2} R_{5} R_{7} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{5} R_{7} R_{9} ea_{1} g_{1} - I_{1} R_{2} R_{5} R_{7} f_{1} - I_{1} R_{2} R_{5} R_{7} + I_{1} R_{2} R_{6} R_{7} R_{8} g_{1} - I_{1} R_{2} R_{6} R_{7} f_{1} - I_{1} R_{2} R_{6} R_{7} + I_{1} R_{2} R_{7} R_{8} R_{9} ea_{1} g_{1} - I_{1} R_{2} R_{7} R_{8} + I_{1} R_{3} R_{5} R_{7} R_{9} ea_{1} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{7} R_{9} ea_{1} g_{1} + I_{1} R_{3} R_{5} R_{7} R_{9} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{7} R_{9} g_{1} + I_{1} R_{3} R_{5} R_{9} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{3} R_{5} R_{9} ea_{1} g_{1} h_{1} + I_{1} R_{3} R_{5} R_{9} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{9} f_{1} + I_{1} R_{3} R_{5} R_{9} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{9} - I_{1} R_{3} R_{6} R_{9} f_{1} - I_{1} R_{3} R_{6} R_{9} + I_{1} R_{3} R_{7} R_{8} R_{9} ea_{1} g_{1} + I_{1} R_{3} R_{7} R_{8} R_{9} g_{1} - I_{1} R_{3} R_{7} R_{9} ea_{1} f_{1} - I_{1} R_{3} R_{7} R_{9} ea_{1} - I_{1} R_{3} R_{7} R_{9} f_{1} - I_{1} R_{3} R_{7} R_{9} + I_{1} R_{3} R_{8} R_{9} ea_{1} g_{1} h_{1} + I_{1} R_{3} R_{8} R_{9} g_{1} h_{1} - I_{1} R_{3} R_{8} R_{9} - I_{1} R_{3} R_{9} ea_{1} f_{1} h_{1} - I_{1} R_{3} R_{9} f_{1} h_{1} - I_{1} R_{5} R_{7} R_{9} f_{1} - I_{1} R_{5} R_{7} R_{9} - I_{1} R_{6} R_{7} R_{9} f_{1} - I_{1} R_{6} R_{7} R_{9} - I_{1} R_{7} R_{8} R_{9} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{6} V_{3} f_{1} g_{1} + R_{10} R_{2} R_{6} V_{3} g_{1} + R_{10} R_{2} R_{7} V_{3} g_{1} + R_{10} R_{2} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{2} R_{6} V_{3} f_{1} g_{1} + R_{11} R_{2} R_{6} V_{3} g_{1} + R_{11} R_{2} R_{7} V_{3} f_{1} g_{1} + R_{11} R_{2} R_{7} V_{3} g_{1} + R_{11} R_{2} V_{3} f_{1} g_{1} h_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{2} R_{3} R_{6} V_{3} f_{1} g_{1} + R_{2} R_{3} R_{6} V_{3} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} g_{1} - R_{2} R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} g_{1} + R_{2} R_{6} R_{7} V_{3} f_{1} g_{1} + R_{2} R_{6} R_{7} V_{3} g_{1} + R_{2} R_{7} R_{8} V_{1} g_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{4} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} ea_{1} - I_{1} R_{10} R_{2} R_{7} ea_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} ea_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{5} R_{6} f_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{10} R_{5} R_{6} + I_{1} R_{10} R_{6} R_{7} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{8} + I_{1} R_{10} R_{6} f_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{11} R_{5} R_{6} f_{1} + I_{1} R_{11} R_{5} R_{6} + I_{1} R_{11} R_{5} R_{7} f_{1} + I_{1} R_{11} R_{5} R_{7} + I_{1} R_{11} R_{6} R_{8} + I_{1} R_{11} R_{7} R_{8} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{5} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{5} R_{7} ea_{1} - I_{1} R_{2} R_{7} R_{8} ea_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} + I_{1} R_{3} R_{5} R_{6} f_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{3} R_{5} R_{6} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} R_{8} + I_{1} R_{3} R_{6} f_{1} h_{1} + I_{1} R_{5} R_{6} R_{7} f_{1} + I_{1} R_{5} R_{6} R_{7} + I_{1} R_{6} R_{7} R_{8} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} + R_{10} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{10} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{3} V_{3} ea_{1} f_{1} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{6} V_{3} f_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} + R_{10} R_{6} V_{3} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} + R_{11} R_{6} V_{3} f_{1} + R_{11} R_{6} V_{3} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{7} V_{3} f_{1} + R_{11} R_{7} V_{3} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{11} V_{3} f_{1} h_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{1} ea_{1} f_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{1} ea_{1} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{3} R_{6} V_{3} f_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{6} V_{3} + R_{3} R_{7} R_{8} V_{1} ea_{1} g_{1} - R_{3} R_{7} V_{1} ea_{1} f_{1} - R_{3} R_{7} V_{1} ea_{1} + R_{3} R_{7} V_{3} ea_{1} f_{1} + R_{3} R_{7} V_{3} ea_{1} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{8} V_{1} ea_{1} - R_{3} V_{1} ea_{1} f_{1} h_{1} + R_{3} V_{3} ea_{1} f_{1} h_{1} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} + R_{6} R_{7} V_{3} f_{1} + R_{6} R_{7} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{5} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{7} ea_{1} f_{1} + I_{1} R_{11} R_{2} R_{7} ea_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} h_{1} + I_{1} R_{11} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} ea_{1} f_{1} + I_{1} R_{11} R_{3} R_{7} ea_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} ea_{1} f_{1} h_{1} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{11} R_{5} R_{6} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{11} R_{5} R_{7} f_{1} + I_{1} R_{11} R_{5} R_{7} + I_{1} R_{11} R_{6} R_{8} g_{1} h_{1} - I_{1} R_{11} R_{6} f_{1} h_{1} + I_{1} R_{11} R_{7} R_{8} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} + R_{11} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{6} V_{3} g_{1} h_{1} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{7} V_{3} f_{1} + R_{11} R_{7} V_{3} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{11} V_{3} f_{1} h_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{6} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{7} ea_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} ea_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{7} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{8} + I_{1} R_{10} R_{6} f_{1} h_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{11} R_{6} R_{8} + I_{1} R_{11} R_{7} R_{8} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{7} R_{8} ea_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} R_{8} + I_{1} R_{3} R_{6} f_{1} h_{1} + I_{1} R_{6} R_{7} R_{8} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} - R_{10} R_{2} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{5} V_{3} ea_{1} g_{1} + R_{10} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{10} R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{3} R_{5} V_{3} ea_{1} g_{1} + R_{10} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{3} V_{3} ea_{1} f_{1} - R_{10} R_{5} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{5} V_{3} f_{1} - R_{10} R_{5} V_{3} g_{1} h_{1} + R_{10} R_{5} V_{3} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{6} V_{3} f_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} + R_{10} R_{6} V_{3} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{2} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{5} V_{3} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{5} V_{3} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{5} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{3} f_{1} - R_{11} R_{5} V_{3} g_{1} h_{1} + R_{11} R_{5} V_{3} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} + R_{11} R_{6} V_{3} f_{1} + R_{11} R_{6} V_{3} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{7} V_{3} f_{1} + R_{11} R_{7} V_{3} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{11} V_{3} f_{1} h_{1} - R_{2} R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{3} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} g_{1} - R_{2} R_{5} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{5} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} g_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{3} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{3} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{3} f_{1} - R_{3} R_{5} V_{3} g_{1} h_{1} + R_{3} R_{5} V_{3} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{3} R_{6} V_{3} f_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{6} V_{3} + R_{3} R_{7} R_{8} V_{1} ea_{1} g_{1} - R_{3} R_{7} V_{1} ea_{1} f_{1} - R_{3} R_{7} V_{1} ea_{1} + R_{3} R_{7} V_{3} ea_{1} f_{1} + R_{3} R_{7} V_{3} ea_{1} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{8} V_{1} ea_{1} - R_{3} V_{1} ea_{1} f_{1} h_{1} + R_{3} V_{3} ea_{1} f_{1} h_{1} - R_{5} R_{7} V_{1} f_{1} - R_{5} R_{7} V_{1} + R_{5} R_{7} V_{3} f_{1} + R_{5} R_{7} V_{3} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} + R_{6} R_{7} V_{3} f_{1} + R_{6} R_{7} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{7} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{7} ea_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{7} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} f_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} + R_{10} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{10} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} - R_{10} R_{7} V_{3} - R_{10} V_{3} f_{1} h_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{7} R_{8} V_{1} ea_{1} g_{1} - R_{3} R_{7} V_{1} ea_{1} f_{1} - R_{3} R_{7} V_{1} ea_{1} - R_{3} R_{7} V_{3} f_{1} - R_{3} R_{7} V_{3} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} V_{1} ea_{1} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1} - R_{5} R_{7} V_{1} f_{1} - R_{5} R_{7} V_{1} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} - R_{7} R_{8} V_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{8} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} + I_{1} R_{10} R_{12} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{12} R_{6} f_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{7} ea_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} ea_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{7} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{8} + I_{1} R_{10} R_{6} f_{1} h_{1} + I_{1} R_{11} R_{12} R_{2} ea_{1} f_{1} + I_{1} R_{11} R_{12} R_{3} ea_{1} f_{1} - I_{1} R_{11} R_{12} R_{6} f_{1} - I_{1} R_{11} R_{12} R_{7} f_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{11} R_{6} R_{8} + I_{1} R_{11} R_{7} R_{8} + I_{1} R_{12} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{12} R_{2} R_{7} ea_{1} f_{1} - I_{1} R_{12} R_{3} R_{6} f_{1} - I_{1} R_{12} R_{6} R_{7} f_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{7} R_{8} ea_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} R_{8} + I_{1} R_{3} R_{6} f_{1} h_{1} + I_{1} R_{6} R_{7} R_{8} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} - R_{10} R_{12} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{12} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{12} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{12} V_{3} f_{1} - R_{10} R_{2} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{5} V_{3} ea_{1} g_{1} + R_{10} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{10} R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{3} R_{5} V_{3} ea_{1} g_{1} + R_{10} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{3} V_{3} ea_{1} f_{1} - R_{10} R_{5} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{5} V_{3} f_{1} - R_{10} R_{5} V_{3} g_{1} h_{1} + R_{10} R_{5} V_{3} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{6} V_{3} f_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} + R_{10} R_{6} V_{3} - R_{11} R_{12} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{12} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{12} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{12} V_{3} f_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{2} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{5} V_{3} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{5} V_{3} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{5} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{3} f_{1} - R_{11} R_{5} V_{3} g_{1} h_{1} + R_{11} R_{5} V_{3} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} + R_{11} R_{6} V_{3} f_{1} + R_{11} R_{6} V_{3} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{7} V_{3} f_{1} + R_{11} R_{7} V_{3} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{11} V_{3} f_{1} h_{1} - R_{12} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{12} R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{12} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{12} R_{3} R_{7} V_{3} f_{1} g_{1} + R_{12} R_{3} V_{1} ea_{1} f_{1} - R_{12} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{12} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{12} R_{3} V_{3} f_{1} - R_{12} R_{7} V_{1} f_{1} + R_{12} R_{7} V_{3} f_{1} - R_{2} R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{3} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} g_{1} - R_{2} R_{5} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{5} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{3} g_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{3} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{3} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{3} f_{1} - R_{3} R_{5} V_{3} g_{1} h_{1} + R_{3} R_{5} V_{3} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{3} R_{6} V_{3} f_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{6} V_{3} + R_{3} R_{7} R_{8} V_{1} ea_{1} g_{1} - R_{3} R_{7} V_{1} ea_{1} f_{1} - R_{3} R_{7} V_{1} ea_{1} + R_{3} R_{7} V_{3} ea_{1} f_{1} + R_{3} R_{7} V_{3} ea_{1} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{8} V_{1} ea_{1} - R_{3} V_{1} ea_{1} f_{1} h_{1} + R_{3} V_{3} ea_{1} f_{1} h_{1} - R_{5} R_{7} V_{1} f_{1} - R_{5} R_{7} V_{1} + R_{5} R_{7} V_{3} f_{1} + R_{5} R_{7} V_{3} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} + R_{6} R_{7} V_{3} f_{1} + R_{6} R_{7} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{9} = \frac{I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{10} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{10} R_{3} R_{6} f_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} g_{1} - R_{10} R_{3} R_{7} V_{3} g_{1} - R_{10} R_{3} V_{3} f_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{2} R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} R_{7} V_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{1} g_{1} - R_{3} R_{5} V_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} f_{1} - R_{3} R_{5} V_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} + R_{3} R_{6} V_{1} f_{1} + R_{3} R_{6} V_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} - R_{3} R_{7} R_{8} V_{1} g_{1} + R_{3} R_{7} V_{1} f_{1} + R_{3} R_{7} V_{1} - R_{3} R_{7} V_{3} f_{1} - R_{3} R_{7} V_{3} - R_{3} R_{8} V_{1} g_{1} h_{1} + R_{3} R_{8} V_{1} + R_{3} V_{1} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{10} = \frac{I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{10} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{10} R_{3} R_{6} f_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{5} V_{2} ea_{1} g_{1} - R_{10} R_{2} R_{8} V_{2} ea_{1} g_{1} - R_{10} R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{10} R_{3} R_{5} V_{2} ea_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} g_{1} - R_{10} R_{3} R_{7} V_{3} g_{1} - R_{10} R_{3} R_{8} V_{2} ea_{1} g_{1} + R_{10} R_{3} V_{2} ea_{1} f_{1} - R_{10} R_{3} V_{3} f_{1} - R_{10} R_{5} V_{2} f_{1} g_{1} h_{1} + R_{10} R_{5} V_{2} f_{1} - R_{10} R_{5} V_{2} g_{1} h_{1} + R_{10} R_{5} V_{2} + R_{10} R_{6} V_{2} f_{1} + R_{10} R_{6} V_{2} + R_{10} R_{7} V_{2} - R_{10} R_{8} V_{2} g_{1} h_{1} + R_{10} R_{8} V_{2} + R_{10} V_{2} f_{1} h_{1} - R_{11} R_{2} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{5} V_{2} ea_{1} g_{1} - R_{11} R_{2} R_{8} V_{2} ea_{1} g_{1} - R_{11} R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{5} V_{2} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} - R_{11} R_{3} R_{8} V_{2} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{2} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{2} f_{1} - R_{11} R_{5} V_{2} g_{1} h_{1} + R_{11} R_{5} V_{2} + R_{11} R_{6} V_{2} f_{1} + R_{11} R_{6} V_{2} + R_{11} R_{7} V_{2} f_{1} + R_{11} R_{7} V_{2} - R_{11} R_{8} V_{2} g_{1} h_{1} + R_{11} R_{8} V_{2} + R_{11} V_{2} f_{1} h_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{2} R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{2} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{2} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{2} R_{3} R_{8} V_{2} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{2} R_{5} R_{7} V_{2} ea_{1} f_{1} g_{1} - R_{2} R_{5} R_{7} V_{2} ea_{1} g_{1} - R_{2} R_{7} R_{8} V_{2} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} ea_{1} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} ea_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} f_{1} g_{1} - R_{3} R_{5} R_{7} V_{2} g_{1} - R_{3} R_{5} V_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} f_{1} - R_{3} R_{5} V_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} - R_{3} R_{5} V_{2} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{2} ea_{1} g_{1} h_{1} - R_{3} R_{5} V_{2} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{2} f_{1} - R_{3} R_{5} V_{2} g_{1} h_{1} + R_{3} R_{5} V_{2} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} + R_{3} R_{6} V_{1} f_{1} + R_{3} R_{6} V_{1} + R_{3} R_{6} V_{2} f_{1} + R_{3} R_{6} V_{2} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} - R_{3} R_{7} R_{8} V_{1} g_{1} - R_{3} R_{7} R_{8} V_{2} ea_{1} g_{1} - R_{3} R_{7} R_{8} V_{2} g_{1} + R_{3} R_{7} V_{1} f_{1} + R_{3} R_{7} V_{1} + R_{3} R_{7} V_{2} ea_{1} f_{1} + R_{3} R_{7} V_{2} ea_{1} + R_{3} R_{7} V_{2} f_{1} + R_{3} R_{7} V_{2} - R_{3} R_{7} V_{3} f_{1} - R_{3} R_{7} V_{3} - R_{3} R_{8} V_{1} g_{1} h_{1} + R_{3} R_{8} V_{1} - R_{3} R_{8} V_{2} ea_{1} g_{1} h_{1} - R_{3} R_{8} V_{2} g_{1} h_{1} + R_{3} R_{8} V_{2} + R_{3} V_{1} f_{1} h_{1} + R_{3} V_{2} ea_{1} f_{1} h_{1} + R_{3} V_{2} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1} + R_{5} R_{7} V_{2} f_{1} + R_{5} R_{7} V_{2} + R_{6} R_{7} V_{2} f_{1} + R_{6} R_{7} V_{2} + R_{7} R_{8} V_{2}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{11} = \frac{I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{10} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{10} R_{3} R_{6} f_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} V_{1} ea_{1} g_{1} + R_{10} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{10} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} g_{1} - R_{10} R_{3} R_{7} V_{3} g_{1} + R_{10} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{10} R_{3} V_{1} ea_{1} f_{1} - R_{10} R_{3} V_{3} f_{1} + R_{10} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{10} R_{5} V_{1} f_{1} + R_{10} R_{5} V_{1} g_{1} h_{1} - R_{10} R_{5} V_{1} - R_{10} R_{6} V_{1} f_{1} - R_{10} R_{6} V_{1} - R_{10} R_{7} V_{1} + R_{10} R_{8} V_{1} g_{1} h_{1} - R_{10} R_{8} V_{1} - R_{10} V_{1} f_{1} h_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{7} R_{8} V_{1} ea_{1} g_{1} - R_{3} R_{7} V_{1} ea_{1} f_{1} - R_{3} R_{7} V_{1} ea_{1} - R_{3} R_{7} V_{3} f_{1} - R_{3} R_{7} V_{3} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} V_{1} ea_{1} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1} - R_{5} R_{7} V_{1} f_{1} - R_{5} R_{7} V_{1} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} - R_{7} R_{8} V_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{12} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{7} ea_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} ea_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{7} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{8} + I_{1} R_{10} R_{6} f_{1} h_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} ea_{1} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{11} R_{6} R_{8} + I_{1} R_{11} R_{7} R_{8} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{7} R_{8} ea_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} R_{8} + I_{1} R_{3} R_{6} f_{1} h_{1} + I_{1} R_{6} R_{7} R_{8} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} + R_{10} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{2} R_{8} V_{3} ea_{1} g_{1} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{10} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{10} R_{3} R_{8} V_{3} ea_{1} g_{1} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} - R_{10} R_{7} V_{3} + R_{10} R_{8} V_{3} g_{1} h_{1} - R_{10} R_{8} V_{3} - R_{10} V_{3} f_{1} h_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{3} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{8} V_{3} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} + R_{11} R_{8} V_{3} g_{1} h_{1} - R_{11} R_{8} V_{3} - R_{11} V_{1} f_{1} h_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} R_{8} V_{3} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{2} R_{7} R_{8} V_{3} ea_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} V_{1} ea_{1} g_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{7} R_{8} V_{1} ea_{1} g_{1} + R_{3} R_{7} R_{8} V_{3} ea_{1} g_{1} + R_{3} R_{7} R_{8} V_{3} g_{1} - R_{3} R_{7} V_{1} ea_{1} f_{1} - R_{3} R_{7} V_{1} ea_{1} - R_{3} R_{7} V_{3} f_{1} - R_{3} R_{7} V_{3} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{8} V_{1} ea_{1} + R_{3} R_{8} V_{3} ea_{1} g_{1} h_{1} + R_{3} R_{8} V_{3} g_{1} h_{1} - R_{3} R_{8} V_{3} - R_{3} V_{1} ea_{1} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1} - R_{5} R_{7} V_{1} f_{1} - R_{5} R_{7} V_{1} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} - R_{7} R_{8} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{13} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} R_{6} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{2} R_{5} R_{6} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{6} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{6} ea_{1} f_{1} + I_{1} R_{10} R_{2} R_{6} ea_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{3} R_{5} R_{6} ea_{1} g_{1} - I_{1} R_{10} R_{3} R_{6} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{3} R_{6} ea_{1} f_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{5} R_{6} f_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{10} R_{5} R_{6} + I_{1} R_{10} R_{6} R_{7} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} R_{8} + I_{1} R_{10} R_{6} f_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} R_{6} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} R_{6} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{6} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{6} ea_{1} f_{1} + I_{1} R_{11} R_{2} R_{6} ea_{1} - I_{1} R_{11} R_{2} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{7} ea_{1} f_{1} + I_{1} R_{11} R_{2} R_{7} ea_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} h_{1} + I_{1} R_{11} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} ea_{1} f_{1} + I_{1} R_{11} R_{3} R_{6} ea_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} ea_{1} f_{1} + I_{1} R_{11} R_{3} R_{7} ea_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} ea_{1} f_{1} h_{1} + I_{1} R_{11} R_{3} f_{1} h_{1} + I_{1} R_{11} R_{5} R_{6} f_{1} + I_{1} R_{11} R_{5} R_{6} + I_{1} R_{11} R_{5} R_{7} f_{1} + I_{1} R_{11} R_{5} R_{7} + I_{1} R_{11} R_{6} R_{8} + I_{1} R_{11} R_{7} R_{8} - I_{1} R_{2} R_{3} R_{5} R_{6} ea_{1} f_{1} g_{1} - I_{1} R_{2} R_{3} R_{5} R_{6} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{6} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{6} ea_{1} f_{1} + I_{1} R_{2} R_{3} R_{6} ea_{1} - I_{1} R_{2} R_{5} R_{6} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{2} R_{5} R_{6} R_{7} ea_{1} g_{1} - I_{1} R_{2} R_{6} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{6} R_{7} ea_{1} f_{1} + I_{1} R_{2} R_{6} R_{7} ea_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} ea_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} f_{1} g_{1} - I_{1} R_{3} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{3} R_{5} R_{6} ea_{1} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} ea_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} + I_{1} R_{3} R_{5} R_{6} f_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{3} R_{5} R_{6} - I_{1} R_{3} R_{6} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{3} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{3} R_{6} R_{7} ea_{1} f_{1} + I_{1} R_{3} R_{6} R_{7} ea_{1} + I_{1} R_{3} R_{6} R_{7} f_{1} + I_{1} R_{3} R_{6} R_{7} - I_{1} R_{3} R_{6} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} R_{8} + I_{1} R_{3} R_{6} ea_{1} f_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} + I_{1} R_{5} R_{6} R_{7} f_{1} + I_{1} R_{5} R_{6} R_{7} + I_{1} R_{6} R_{7} R_{8} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} - R_{10} R_{2} R_{6} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{2} R_{6} V_{3} ea_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{3} R_{6} V_{3} ea_{1} g_{1} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{6} V_{3} f_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} + R_{10} R_{6} V_{3} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{2} R_{6} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{6} V_{3} ea_{1} g_{1} - R_{11} R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} + R_{11} R_{6} V_{3} f_{1} + R_{11} R_{6} V_{3} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} + R_{11} R_{7} V_{3} f_{1} + R_{11} R_{7} V_{3} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{11} V_{3} f_{1} h_{1} - R_{2} R_{3} R_{6} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{6} V_{3} ea_{1} g_{1} - R_{2} R_{6} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{6} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} f_{1} g_{1} - R_{3} R_{6} R_{7} V_{3} g_{1} + R_{3} R_{6} V_{1} ea_{1} f_{1} + R_{3} R_{6} V_{1} ea_{1} - R_{3} R_{6} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} ea_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} + R_{3} R_{6} V_{3} f_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} + R_{3} R_{6} V_{3} - R_{6} R_{7} V_{1} f_{1} - R_{6} R_{7} V_{1} + R_{6} R_{7} V_{3} f_{1} + R_{6} R_{7} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{14} = \frac{- I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{10} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} f_{1} - I_{1} R_{10} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{5} + I_{1} R_{10} R_{11} R_{6} + I_{1} R_{10} R_{11} R_{7} - I_{1} R_{10} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{11} R_{8} + I_{1} R_{10} R_{11} f_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{10} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{10} R_{6} f_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{7} ea_{1} f_{1} + I_{1} R_{11} R_{2} R_{7} ea_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{6} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} R_{7} g_{1} - I_{1} R_{11} R_{3} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} f_{1} - I_{1} R_{11} R_{3} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{5} - I_{1} R_{11} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{6} f_{1} + I_{1} R_{11} R_{3} R_{6} - I_{1} R_{11} R_{3} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{7} R_{8} g_{1} + I_{1} R_{11} R_{3} R_{7} ea_{1} f_{1} + I_{1} R_{11} R_{3} R_{7} ea_{1} + I_{1} R_{11} R_{3} R_{7} f_{1} + I_{1} R_{11} R_{3} R_{7} - I_{1} R_{11} R_{3} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{3} R_{8} + I_{1} R_{11} R_{3} f_{1} h_{1} - I_{1} R_{11} R_{5} R_{7} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{5} R_{7} f_{1} - I_{1} R_{11} R_{5} R_{7} g_{1} h_{1} + I_{1} R_{11} R_{5} R_{7} - I_{1} R_{11} R_{7} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{7} R_{8} + I_{1} R_{11} R_{7} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} + I_{1} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{5} R_{7} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{7} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{7} ea_{1} f_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{3} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{3} R_{6} f_{1} h_{1} - I_{1} R_{5} R_{6} R_{7} f_{1} g_{1} h_{1} - I_{1} R_{5} R_{6} R_{7} g_{1} h_{1} - I_{1} R_{6} R_{7} R_{8} g_{1} h_{1} + I_{1} R_{6} R_{7} f_{1} h_{1} - R_{10} R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{11} V_{3} f_{1} g_{1} h_{1} + R_{10} R_{11} V_{3} f_{1} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{10} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{10} R_{6} V_{3} g_{1} h_{1} - R_{10} R_{7} V_{3} g_{1} h_{1} - R_{10} V_{3} f_{1} h_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{11} R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} V_{1} ea_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{6} V_{3} g_{1} - R_{11} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} f_{1} g_{1} - R_{11} R_{3} R_{7} V_{3} g_{1} + R_{11} R_{3} R_{8} V_{1} ea_{1} g_{1} - R_{11} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{5} V_{1} f_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} f_{1} + R_{11} R_{5} V_{1} g_{1} h_{1} - R_{11} R_{5} V_{1} - R_{11} R_{6} V_{1} f_{1} - R_{11} R_{6} V_{1} - R_{11} R_{7} V_{1} f_{1} - R_{11} R_{7} V_{1} - R_{11} R_{7} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{7} V_{3} f_{1} - R_{11} R_{7} V_{3} g_{1} h_{1} + R_{11} R_{7} V_{3} + R_{11} R_{8} V_{1} g_{1} h_{1} - R_{11} R_{8} V_{1} - R_{11} V_{1} f_{1} h_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} V_{1} ea_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} f_{1} g_{1} h_{1} - R_{3} R_{6} V_{3} g_{1} h_{1} - R_{3} R_{7} V_{3} ea_{1} g_{1} h_{1} - R_{3} R_{7} V_{3} g_{1} h_{1} + R_{3} R_{8} V_{1} ea_{1} g_{1} h_{1} - R_{3} V_{1} ea_{1} f_{1} h_{1} - R_{3} V_{3} f_{1} h_{1} - R_{5} R_{7} V_{1} f_{1} g_{1} h_{1} - R_{5} R_{7} V_{1} g_{1} h_{1} - R_{6} R_{7} V_{3} f_{1} g_{1} h_{1} - R_{6} R_{7} V_{3} g_{1} h_{1} - R_{7} R_{8} V_{1} g_{1} h_{1} + R_{7} V_{1} f_{1} h_{1} - R_{7} V_{3} f_{1} h_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(v_{15} = \frac{- I_{1} R_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{1} R_{10} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{1} R_{10} R_{5} R_{6} g_{1} + I_{1} R_{1} R_{10} R_{6} R_{8} g_{1} - I_{1} R_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} - I_{1} R_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{1} R_{11} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{1} R_{11} R_{5} R_{6} g_{1} + I_{1} R_{1} R_{11} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{1} R_{11} R_{5} R_{7} g_{1} + I_{1} R_{1} R_{11} R_{6} R_{8} g_{1} + I_{1} R_{1} R_{11} R_{7} R_{8} g_{1} - I_{1} R_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{1} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{1} R_{2} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{1} R_{2} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{1} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{1} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{1} R_{3} R_{6} R_{8} g_{1} + I_{1} R_{1} R_{5} R_{6} R_{7} f_{1} g_{1} + I_{1} R_{1} R_{5} R_{6} R_{7} g_{1} + I_{1} R_{1} R_{6} R_{7} R_{8} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{10} R_{2} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{5} R_{6} g_{1} + I_{1} R_{10} R_{2} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} f_{1} + I_{1} R_{10} R_{2} R_{5} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{5} + I_{1} R_{10} R_{2} R_{6} R_{8} g_{1} - I_{1} R_{10} R_{2} R_{6} f_{1} - I_{1} R_{10} R_{2} R_{6} - I_{1} R_{10} R_{2} R_{7} + I_{1} R_{10} R_{2} R_{8} g_{1} h_{1} - I_{1} R_{10} R_{2} R_{8} - I_{1} R_{10} R_{2} f_{1} h_{1} + I_{1} R_{11} R_{2} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{6} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} R_{7} g_{1} + I_{1} R_{11} R_{2} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} f_{1} + I_{1} R_{11} R_{2} R_{5} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{5} + I_{1} R_{11} R_{2} R_{6} R_{8} g_{1} - I_{1} R_{11} R_{2} R_{6} f_{1} - I_{1} R_{11} R_{2} R_{6} + I_{1} R_{11} R_{2} R_{7} R_{8} g_{1} - I_{1} R_{11} R_{2} R_{7} f_{1} - I_{1} R_{11} R_{2} R_{7} + I_{1} R_{11} R_{2} R_{8} g_{1} h_{1} - I_{1} R_{11} R_{2} R_{8} - I_{1} R_{11} R_{2} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} R_{7} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} f_{1} + I_{1} R_{2} R_{3} R_{5} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} + I_{1} R_{2} R_{3} R_{6} R_{8} g_{1} - I_{1} R_{2} R_{3} R_{6} f_{1} - I_{1} R_{2} R_{3} R_{6} + I_{1} R_{2} R_{3} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{7} R_{8} g_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{3} R_{7} ea_{1} - I_{1} R_{2} R_{3} R_{7} f_{1} - I_{1} R_{2} R_{3} R_{7} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{3} R_{8} g_{1} h_{1} - I_{1} R_{2} R_{3} R_{8} - I_{1} R_{2} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{2} R_{3} f_{1} h_{1} + I_{1} R_{2} R_{5} R_{6} R_{7} f_{1} g_{1} + I_{1} R_{2} R_{5} R_{6} R_{7} g_{1} - I_{1} R_{2} R_{5} R_{7} f_{1} - I_{1} R_{2} R_{5} R_{7} + I_{1} R_{2} R_{6} R_{7} R_{8} g_{1} - I_{1} R_{2} R_{6} R_{7} f_{1} - I_{1} R_{2} R_{6} R_{7} - I_{1} R_{2} R_{7} R_{8} + R_{1} R_{10} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{1} R_{10} R_{6} V_{3} f_{1} g_{1} + R_{1} R_{10} R_{6} V_{3} g_{1} + R_{1} R_{10} R_{7} V_{3} g_{1} + R_{1} R_{10} V_{3} f_{1} g_{1} h_{1} + R_{1} R_{11} R_{6} V_{3} f_{1} g_{1} + R_{1} R_{11} R_{6} V_{3} g_{1} + R_{1} R_{11} R_{7} V_{3} f_{1} g_{1} + R_{1} R_{11} R_{7} V_{3} g_{1} + R_{1} R_{11} V_{3} f_{1} g_{1} h_{1} - R_{1} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{1} R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{1} R_{3} R_{6} V_{3} f_{1} g_{1} + R_{1} R_{3} R_{6} V_{3} g_{1} + R_{1} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{1} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{1} R_{3} R_{7} V_{3} f_{1} g_{1} + R_{1} R_{3} R_{7} V_{3} g_{1} - R_{1} R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{1} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{1} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{1} R_{5} R_{7} V_{1} f_{1} g_{1} + R_{1} R_{5} R_{7} V_{1} g_{1} + R_{1} R_{6} R_{7} V_{3} f_{1} g_{1} + R_{1} R_{6} R_{7} V_{3} g_{1} + R_{1} R_{7} R_{8} V_{1} g_{1} + R_{10} R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{6} V_{3} f_{1} g_{1} + R_{10} R_{2} R_{6} V_{3} g_{1} + R_{10} R_{2} R_{7} V_{3} g_{1} + R_{10} R_{2} V_{3} f_{1} g_{1} h_{1} + R_{11} R_{2} R_{6} V_{3} f_{1} g_{1} + R_{11} R_{2} R_{6} V_{3} g_{1} + R_{11} R_{2} R_{7} V_{3} f_{1} g_{1} + R_{11} R_{2} R_{7} V_{3} g_{1} + R_{11} R_{2} V_{3} f_{1} g_{1} h_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{2} R_{3} R_{6} V_{3} f_{1} g_{1} + R_{2} R_{3} R_{6} V_{3} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} f_{1} g_{1} + R_{2} R_{3} R_{7} V_{3} g_{1} - R_{2} R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{2} R_{3} V_{3} f_{1} g_{1} h_{1} + R_{2} R_{5} R_{7} V_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} V_{1} g_{1} + R_{2} R_{6} R_{7} V_{3} f_{1} g_{1} + R_{2} R_{6} R_{7} V_{3} g_{1} + R_{2} R_{7} R_{8} V_{1} g_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(I_{V1} = \frac{- I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{5} f_{1} - I_{1} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{5} + I_{1} R_{11} R_{6} + I_{1} R_{11} R_{7} - I_{1} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{8} + I_{1} R_{11} f_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{5} ea_{1} g_{1} h_{1} - I_{1} R_{2} R_{7} ea_{1} + I_{1} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} ea_{1} f_{1} h_{1} + I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{3} R_{6} R_{8} g_{1} - I_{1} R_{3} R_{6} f_{1} - I_{1} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{5} R_{6} g_{1} h_{1} + I_{1} R_{6} R_{7} - I_{1} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{6} f_{1} h_{1} - R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{11} V_{3} f_{1} g_{1} h_{1} + R_{11} V_{3} f_{1} - R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{5} V_{1} ea_{1} g_{1} + R_{2} R_{7} V_{3} ea_{1} g_{1} - R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{3} R_{6} V_{3} f_{1} g_{1} + R_{3} R_{6} V_{3} g_{1} + R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{3} R_{7} V_{3} g_{1} - R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{3} V_{1} ea_{1} f_{1} + R_{3} V_{3} f_{1} - R_{5} V_{1} f_{1} g_{1} h_{1} + R_{5} V_{1} f_{1} - R_{5} V_{1} g_{1} h_{1} + R_{5} V_{1} + R_{6} V_{1} f_{1} + R_{6} V_{1} - R_{6} V_{3} f_{1} g_{1} h_{1} - R_{6} V_{3} g_{1} h_{1} + R_{7} V_{1} - R_{7} V_{3} - R_{8} V_{1} g_{1} h_{1} + R_{8} V_{1} + V_{1} f_{1} h_{1} - V_{3} f_{1} h_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(I_{V2} = \frac{- I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{10} R_{2} ea_{1} f_{1} + I_{1} R_{10} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{10} R_{5} R_{6} g_{1} + I_{1} R_{10} R_{6} R_{8} g_{1} - I_{1} R_{10} R_{6} f_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{3} ea_{1} f_{1} + I_{1} R_{11} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{11} R_{5} R_{6} g_{1} + I_{1} R_{11} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{11} R_{5} R_{7} g_{1} + I_{1} R_{11} R_{6} R_{8} g_{1} - I_{1} R_{11} R_{6} f_{1} + I_{1} R_{11} R_{7} R_{8} g_{1} - I_{1} R_{11} R_{7} f_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} ea_{1} f_{1} - I_{1} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} - I_{1} R_{2} R_{5} R_{7} ea_{1} g_{1} - I_{1} R_{2} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{7} ea_{1} f_{1} + I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{3} R_{6} R_{8} g_{1} - I_{1} R_{3} R_{6} f_{1} + I_{1} R_{5} R_{6} R_{7} f_{1} g_{1} + I_{1} R_{5} R_{6} R_{7} g_{1} + I_{1} R_{6} R_{7} R_{8} g_{1} - I_{1} R_{6} R_{7} f_{1} - R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{6} V_{3} f_{1} g_{1} + R_{10} R_{6} V_{3} g_{1} + R_{10} R_{7} V_{3} g_{1} + R_{10} V_{3} f_{1} - R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{11} R_{6} V_{3} f_{1} g_{1} + R_{11} R_{6} V_{3} g_{1} + R_{11} R_{7} V_{3} f_{1} g_{1} + R_{11} R_{7} V_{3} g_{1} + R_{11} V_{3} f_{1} - R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{3} R_{6} V_{3} f_{1} g_{1} + R_{3} R_{6} V_{3} g_{1} + R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{3} R_{7} V_{3} g_{1} - R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{3} V_{1} ea_{1} f_{1} + R_{3} V_{3} f_{1} + R_{5} R_{7} V_{1} f_{1} g_{1} + R_{5} R_{7} V_{1} g_{1} + R_{6} R_{7} V_{3} f_{1} g_{1} + R_{6} R_{7} V_{3} g_{1} + R_{7} R_{8} V_{1} g_{1} - R_{7} V_{1} f_{1} + R_{7} V_{3} f_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(I_{V3} = \frac{I_{1} R_{10} R_{2} ea_{1} - I_{1} R_{10} R_{6} + I_{1} R_{11} R_{2} ea_{1} + I_{1} R_{11} R_{3} ea_{1} - I_{1} R_{11} R_{6} - I_{1} R_{11} R_{7} + I_{1} R_{2} R_{3} ea_{1} + I_{1} R_{2} R_{7} ea_{1} - I_{1} R_{3} R_{6} - I_{1} R_{6} R_{7} - R_{10} R_{2} V_{3} ea_{1} g_{1} - R_{10} R_{3} V_{3} ea_{1} g_{1} - R_{10} V_{3} g_{1} h_{1} + R_{10} V_{3} - R_{11} R_{2} V_{3} ea_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} g_{1} - R_{11} V_{3} g_{1} h_{1} + R_{11} V_{3} - R_{2} R_{3} V_{3} ea_{1} g_{1} - R_{2} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{7} V_{3} ea_{1} g_{1} - R_{3} R_{7} V_{3} g_{1} + R_{3} V_{1} ea_{1} - R_{3} V_{3} ea_{1} g_{1} h_{1} - R_{3} V_{3} g_{1} h_{1} + R_{3} V_{3} - R_{7} V_{1} + R_{7} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(I_{Ea1} = \frac{I_{1} R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{2} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{2} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{2} ea_{1} + I_{1} R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{10} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{10} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{10} R_{3} ea_{1} f_{1} + I_{1} R_{10} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{10} R_{5} f_{1} + I_{1} R_{10} R_{5} g_{1} h_{1} - I_{1} R_{10} R_{5} - I_{1} R_{10} R_{7} + I_{1} R_{10} R_{8} g_{1} h_{1} - I_{1} R_{10} R_{8} - I_{1} R_{10} f_{1} h_{1} + I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} + I_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{2} ea_{1} f_{1} - I_{1} R_{11} R_{2} ea_{1} + I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{11} R_{3} ea_{1} + I_{1} R_{11} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{11} R_{5} f_{1} + I_{1} R_{11} R_{5} g_{1} h_{1} - I_{1} R_{11} R_{5} + I_{1} R_{11} R_{8} g_{1} h_{1} - I_{1} R_{11} R_{8} - I_{1} R_{11} f_{1} h_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} + I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{3} ea_{1} f_{1} - I_{1} R_{2} R_{3} ea_{1} + I_{1} R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{2} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{2} R_{7} R_{8} ea_{1} g_{1} - I_{1} R_{2} R_{7} ea_{1} f_{1} - I_{1} R_{2} R_{7} ea_{1} + I_{1} R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{7} ea_{1} g_{1} + I_{1} R_{3} R_{5} R_{7} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{7} g_{1} + I_{1} R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{3} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{3} R_{5} f_{1} g_{1} h_{1} - I_{1} R_{3} R_{5} f_{1} + I_{1} R_{3} R_{5} g_{1} h_{1} - I_{1} R_{3} R_{5} + I_{1} R_{3} R_{7} R_{8} ea_{1} g_{1} + I_{1} R_{3} R_{7} R_{8} g_{1} - I_{1} R_{3} R_{7} ea_{1} f_{1} - I_{1} R_{3} R_{7} ea_{1} - I_{1} R_{3} R_{7} f_{1} - I_{1} R_{3} R_{7} + I_{1} R_{3} R_{8} ea_{1} g_{1} h_{1} + I_{1} R_{3} R_{8} g_{1} h_{1} - I_{1} R_{3} R_{8} - I_{1} R_{3} ea_{1} f_{1} h_{1} - I_{1} R_{3} f_{1} h_{1} - I_{1} R_{5} R_{7} f_{1} - I_{1} R_{5} R_{7} - I_{1} R_{7} R_{8} + R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{2} V_{3} ea_{1} g_{1} + R_{10} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{10} R_{3} V_{3} ea_{1} g_{1} + R_{10} V_{3} f_{1} g_{1} h_{1} - R_{10} V_{3} f_{1} + R_{10} V_{3} g_{1} h_{1} - R_{10} V_{3} + R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} + R_{11} R_{2} V_{3} ea_{1} g_{1} + R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{11} R_{3} V_{3} ea_{1} g_{1} + R_{11} V_{3} f_{1} g_{1} h_{1} - R_{11} V_{3} f_{1} + R_{11} V_{3} g_{1} h_{1} - R_{11} V_{3} + R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{3} V_{3} ea_{1} g_{1} + R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{2} R_{7} V_{3} ea_{1} g_{1} + R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} + R_{3} R_{7} V_{3} ea_{1} g_{1} + R_{3} R_{7} V_{3} f_{1} g_{1} + R_{3} R_{7} V_{3} g_{1} - R_{3} V_{1} ea_{1} f_{1} - R_{3} V_{1} ea_{1} + R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} + R_{3} V_{3} ea_{1} g_{1} h_{1} + R_{3} V_{3} f_{1} g_{1} h_{1} - R_{3} V_{3} f_{1} + R_{3} V_{3} g_{1} h_{1} - R_{3} V_{3} + R_{7} V_{1} f_{1} + R_{7} V_{1} - R_{7} V_{3} f_{1} - R_{7} V_{3}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(I_{F1} = \frac{I_{1} R_{10} R_{2} ea_{1} f_{1} - I_{1} R_{10} R_{6} f_{1} + I_{1} R_{11} R_{2} ea_{1} f_{1} + I_{1} R_{11} R_{3} ea_{1} f_{1} - I_{1} R_{11} R_{6} f_{1} - I_{1} R_{11} R_{7} f_{1} + I_{1} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{2} R_{7} ea_{1} f_{1} - I_{1} R_{3} R_{6} f_{1} - I_{1} R_{6} R_{7} f_{1} - R_{10} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{10} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{10} V_{3} f_{1} g_{1} h_{1} + R_{10} V_{3} f_{1} - R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{11} V_{3} f_{1} g_{1} h_{1} + R_{11} V_{3} f_{1} - R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{3} R_{7} V_{3} ea_{1} f_{1} g_{1} - R_{3} R_{7} V_{3} f_{1} g_{1} + R_{3} V_{1} ea_{1} f_{1} - R_{3} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} V_{3} f_{1} g_{1} h_{1} + R_{3} V_{3} f_{1} - R_{7} V_{1} f_{1} + R_{7} V_{3} f_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)
\(I_{H1} = \frac{I_{1} R_{10} R_{2} ea_{1} - I_{1} R_{10} R_{6} - I_{1} R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{2} R_{5} ea_{1} g_{1} - I_{1} R_{11} R_{2} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{2} ea_{1} f_{1} + I_{1} R_{11} R_{2} ea_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{11} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{11} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{11} R_{3} ea_{1} f_{1} + I_{1} R_{11} R_{3} ea_{1} - I_{1} R_{11} R_{5} f_{1} g_{1} h_{1} + I_{1} R_{11} R_{5} f_{1} - I_{1} R_{11} R_{5} g_{1} h_{1} + I_{1} R_{11} R_{5} - I_{1} R_{11} R_{8} g_{1} h_{1} + I_{1} R_{11} R_{8} + I_{1} R_{11} f_{1} h_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} - I_{1} R_{2} R_{3} R_{5} ea_{1} g_{1} - I_{1} R_{2} R_{3} R_{8} ea_{1} g_{1} + I_{1} R_{2} R_{3} ea_{1} f_{1} + I_{1} R_{2} R_{3} ea_{1} + I_{1} R_{2} R_{5} ea_{1} f_{1} g_{1} h_{1} + I_{1} R_{2} R_{5} ea_{1} g_{1} h_{1} + I_{1} R_{2} R_{8} ea_{1} g_{1} h_{1} - I_{1} R_{2} ea_{1} f_{1} h_{1} + I_{1} R_{3} R_{5} R_{6} f_{1} g_{1} + I_{1} R_{3} R_{5} R_{6} g_{1} + I_{1} R_{3} R_{6} R_{8} g_{1} - I_{1} R_{3} R_{6} f_{1} - I_{1} R_{3} R_{6} - I_{1} R_{5} R_{6} f_{1} g_{1} h_{1} - I_{1} R_{5} R_{6} g_{1} h_{1} - I_{1} R_{6} R_{8} g_{1} h_{1} + I_{1} R_{6} f_{1} h_{1} - R_{10} R_{2} V_{3} ea_{1} g_{1} - R_{10} R_{3} V_{3} ea_{1} g_{1} - R_{10} V_{3} g_{1} h_{1} + R_{10} V_{3} - R_{11} R_{2} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{2} V_{3} ea_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{11} R_{3} V_{3} ea_{1} g_{1} - R_{11} V_{3} f_{1} g_{1} h_{1} + R_{11} V_{3} f_{1} - R_{11} V_{3} g_{1} h_{1} + R_{11} V_{3} - R_{2} R_{3} V_{3} ea_{1} f_{1} g_{1} - R_{2} R_{3} V_{3} ea_{1} g_{1} - R_{2} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{2} R_{5} V_{1} ea_{1} g_{1} - R_{2} R_{8} V_{1} ea_{1} g_{1} + R_{2} V_{3} ea_{1} f_{1} g_{1} h_{1} - R_{3} R_{5} V_{1} ea_{1} f_{1} g_{1} - R_{3} R_{5} V_{1} ea_{1} g_{1} + R_{3} R_{6} V_{3} f_{1} g_{1} + R_{3} R_{6} V_{3} g_{1} - R_{3} R_{8} V_{1} ea_{1} g_{1} + R_{3} V_{1} ea_{1} f_{1} + R_{3} V_{1} ea_{1} - R_{3} V_{3} ea_{1} g_{1} h_{1} + R_{3} V_{3} f_{1} - R_{3} V_{3} g_{1} h_{1} + R_{3} V_{3} - R_{5} V_{1} f_{1} g_{1} h_{1} + R_{5} V_{1} f_{1} - R_{5} V_{1} g_{1} h_{1} + R_{5} V_{1} + R_{6} V_{1} f_{1} + R_{6} V_{1} - R_{6} V_{3} f_{1} g_{1} h_{1} - R_{6} V_{3} g_{1} h_{1} - R_{8} V_{1} g_{1} h_{1} + R_{8} V_{1} + V_{1} f_{1} h_{1} - V_{3} f_{1} h_{1}}{R_{10} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{2} R_{5} ea_{1} g_{1} + R_{10} R_{2} R_{8} ea_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{10} R_{3} R_{5} ea_{1} g_{1} + R_{10} R_{3} R_{8} ea_{1} g_{1} - R_{10} R_{3} ea_{1} f_{1} + R_{10} R_{5} f_{1} g_{1} h_{1} - R_{10} R_{5} f_{1} + R_{10} R_{5} g_{1} h_{1} - R_{10} R_{5} - R_{10} R_{6} f_{1} - R_{10} R_{6} - R_{10} R_{7} + R_{10} R_{8} g_{1} h_{1} - R_{10} R_{8} - R_{10} f_{1} h_{1} + R_{11} R_{2} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{2} R_{5} ea_{1} g_{1} + R_{11} R_{2} R_{8} ea_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{11} R_{3} R_{5} ea_{1} g_{1} + R_{11} R_{3} R_{8} ea_{1} g_{1} + R_{11} R_{5} f_{1} g_{1} h_{1} - R_{11} R_{5} f_{1} + R_{11} R_{5} g_{1} h_{1} - R_{11} R_{5} - R_{11} R_{6} f_{1} - R_{11} R_{6} - R_{11} R_{7} f_{1} - R_{11} R_{7} + R_{11} R_{8} g_{1} h_{1} - R_{11} R_{8} - R_{11} f_{1} h_{1} + R_{2} R_{3} R_{5} ea_{1} f_{1} g_{1} + R_{2} R_{3} R_{5} ea_{1} g_{1} + R_{2} R_{3} R_{8} ea_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{2} R_{5} R_{7} ea_{1} g_{1} + R_{2} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} f_{1} g_{1} + R_{3} R_{5} R_{7} ea_{1} g_{1} + R_{3} R_{5} R_{7} f_{1} g_{1} + R_{3} R_{5} R_{7} g_{1} + R_{3} R_{5} ea_{1} f_{1} g_{1} h_{1} + R_{3} R_{5} ea_{1} g_{1} h_{1} + R_{3} R_{5} f_{1} g_{1} h_{1} - R_{3} R_{5} f_{1} + R_{3} R_{5} g_{1} h_{1} - R_{3} R_{5} - R_{3} R_{6} f_{1} - R_{3} R_{6} + R_{3} R_{7} R_{8} ea_{1} g_{1} + R_{3} R_{7} R_{8} g_{1} - R_{3} R_{7} ea_{1} f_{1} - R_{3} R_{7} ea_{1} - R_{3} R_{7} f_{1} - R_{3} R_{7} + R_{3} R_{8} ea_{1} g_{1} h_{1} + R_{3} R_{8} g_{1} h_{1} - R_{3} R_{8} - R_{3} ea_{1} f_{1} h_{1} - R_{3} f_{1} h_{1} - R_{5} R_{7} f_{1} - R_{5} R_{7} - R_{6} R_{7} f_{1} - R_{6} R_{7} - R_{7} R_{8}}\)

The symbolic solutions for the node voltages and unknown currents shown above are long and appear to be void of any explanatory power. Nevertheless, it is remarkable that these technically correct equations can be generated with almost no effort. In some cases these equations can be useful if some of the component values can be substituted into the equations and some simplification can occur.

Find the DC operating point for the circuit.

NE = NE_sym.subs(element_values) # put the element values into the network equations

# display the equations with numeric values.
temp = ''
for i in range(shape(NE.lhs)[0]):
    temp += '${:s} = {:s}$<br>'.format(latex(NE.rhs[i]),latex(NE.lhs[i]))

Markdown(temp)

\(0 = I_{F1} + 0.333333333333333 v_{1} - 0.333333333333333 v_{10} + 3.0 v_{4} - 3.0 v_{7}\)
\(0 = - 0.5 v_{15} + 0.976190476190476 v_{2} - 0.142857142857143 v_{3}\)
\(2.0 = - 0.142857142857143 v_{2} + 0.142857142857143 v_{3}\)
\(-2.0 = - I_{Ea1} + 0.333333333333333 v_{4} - 0.333333333333333 v_{6}\)
\(0 = I_{H1} - 0.333333333333333 v_{13} + 0.444444444444444 v_{5}\)
\(0 = - I_{V3} - 0.333333333333333 v_{4} + 0.666666666666667 v_{6} - 0.333333333333333 v_{8}\)
\(0 = - 0.25 v_{11} - 0.2 v_{12} - 0.5 v_{14} + 0.95 v_{7}\)
\(0 = - I_{F1} - 0.333333333333333 v_{6} + 0.333333333333333 v_{8}\)
\(0 = - I_{V1} + I_{V2} + 0.25 v_{9}\)
\(0 = - I_{V2} - 0.333333333333333 v_{1} + 0.333333333333333 v_{10}\)
\(0 = I_{V1} + 0.25 v_{11} - 0.25 v_{7}\)
\(0 = I_{V3} + 0.2 v_{12} - 0.2 v_{7}\)
\(0 = I_{Ea1} + 0.333333333333333 v_{13} - 0.333333333333333 v_{5}\)
\(0 = - I_{H1} + 0.5 v_{14} - 0.5 v_{7}\)
\(0 = 0.5 v_{15} - 0.5 v_{2} - 3.0 v_{4} + 3.0 v_{7}\)
\(3.0 = v_{11} - v_{9}\)
\(0 = - v_{10} + v_{9}\)
\(0 = v_{12} - v_{6}\)
\(0 = v_{13} + 2.0 v_{2} - v_{4} - 2.0 v_{9}\)
\(0 = I_{F1} - 2.0 I_{V3}\)
\(0 = - 3.0 I_{V2} - v_{14} + v_{5}\)

Solve for voltages and currents.

U = solve(NE,X)

The following code display the numerical solution. Six significant digits are displayed so that results can be compared to LTSpice.

table_header = ['unknown', 'value','unit']
table_row = []

for name, value in U.items():
    if str(name)[0] == 'I':
        unit = 'device current'
    else:
        unit = 'voltage'
    table_row.append([str(name),float(value),str(unit)])

print(tabulate(table_row, headers=table_header,colalign = ('right','decimal','left'),
    tablefmt="simple",floatfmt=('5s','.6f','20s')))

  unknown       value  unit
---------  ----------  --------------
       v1    0.845718  voltage
       v2    3.586400  voltage
       v3   17.586400  voltage
       v4   -3.238966  voltage
       v5   -7.490063  voltage
       v6   -3.066566  voltage
       v7   -2.970788  voltage
       v8   -2.951632  voltage
       v9   -1.452949  voltage
      v10   -1.452949  voltage
      v11    1.547051  voltage
      v12   -3.066566  voltage
      v13  -13.317663  voltage
      v14   -5.191396  voltage
      v15    1.977333  voltage
     I_V1   -1.129460  device current
     I_V2   -0.766222  device current
     I_V3    0.019156  device current
    I_Ea1    1.942533  device current
     I_F1    0.038311  device current
     I_H1   -1.110304  device current

The Sympy generated solution matches the LTSpice results:

V(2):    3.5864  voltage
V(15):   1.97733     voltage
V(9):    -1.45295    voltage
V(1):    0.845718    voltage
V(10):   -1.45295    voltage
V(4):    -3.23897    voltage
V(6):    -3.06657    voltage
V(5):    -7.49006    voltage
V(13):   -13.3177    voltage
V(7):    -2.97079    voltage
V(14):   -5.1914     voltage
V(12):   -3.06657    voltage
V(3):    17.5864     voltage
V(11):   1.54705     voltage
V(8):    -2.95163    voltage
I(F1):   0.0383111   device_current
I(H1):   -1.1103     device_current
I(I1):   2   device_current
I(R1):   0.804533    device_current
I(R2):   -1.19547    device_current
I(R3):   -0.363237   device_current
I(R4):   0.766222    device_current
I(R5):   -0.0574667  device_current
I(R6):   1.94253     device_current
I(R7):   1.1103  device_current
I(R8):   -0.0191556  device_current
I(R9):   2   device_current
I(R10):  -1.12946    device_current
I(R11):  -0.832229   device_current
I(R12):  -0.0383111  device_current
I(G1):   -0.804533   device_current
I(E1):   1.94253     device_current
I(V1):   -1.12946    device_current
I(V2):   -0.766222   device_current
I(V3):   0.0191556   device_current

5.3 Example Circuit 3

The schematic shown in Figure 5.3 is ment to represent a wheel shaped spider web known as an Orb web. A resistor in the schematic is connected between each junction in the web. The web is connected to ground at three of the corners. The schematic was drawn using LTSpice which places components either horizontally or verticaly, so it was not possible to have the resistors aling with radial lines that would be present in an Orb Web. The schematic is my best attempt to position all the resistors along radial paths.

The network has 45 branches, 22 nodes and 44 resistors. For simplicity all the resistor values are set equal to \(1 \Omega\) in the schematic.

Figure 5.3: Schematic for example 3.

In the schematic, LTSpice assigned the node numbers, which have not been labled in Figure 5.3. Within LTSpice, if the mouse pointer hovers over a node, the node number is displayed in the lower left corner. As you can see, LTSpice numbers the nodes as N001, N002, …

net_list = '''
R1 N005 N010 1
R2 N010 N015 1
R3 N007 N012 1
R4 N012 N017 1
R5 N006 N005 1
R6 N007 N006 1
R7 N016 N015 1
R8 N017 N016 1
R9 N011 N010 1
R10 N012 N011 1
R11 N011 N006 1
R12 N016 N011 1
I1 0 N011 1
R13 N004 N013 1
R14 N013 N020 1
R15 N009 N018 1
R16 N002 N009 1
R17 N010 N009 1
R18 N013 N012 1
R19 N019 N016 1
R20 N006 N003 1
R21 N002 N003 1
R22 N003 N004 1
R23 N019 N020 1
R24 N018 N019 1
R25 N015 N018 1
R26 N017 N020 1
R27 N004 N007 1
R28 N002 N005 1
R29 0 N008 1
R30 N008 0 1
R31 N014 N022 1
R32 0 N014 1
R33 0 N001 1
R34 N001 0 1
R35 N021 0 1
R36 N022 N021 1
R37 N022 N020 1
R38 0 N018 1
R39 N002 0 1
R40 N004 0 1
R41 N003 N001 1
R42 N021 N019 1
R43 N013 N014 1
R44 N008 N009 1
'''

Using the following code, the netlist was modified to use integer values for the node numbers. The Python re library was used to find and replace the LTSpice assigned node labels in the netlist above with a replacement string consisting of digits. Leading zeros in the replacement node labels are ignored in the parser when the ascii digits are converted to integers.

# Pattern: 'N' followed by one or more digits
pattern = r"N(\d+)"

# Replacement: use the captured group 1 (the digits)
replacement = r"\1"

modified_net_list = re.sub(pattern, replacement, net_list)

Generate and display the network equations.

report, network_df, i_unk_df, A, X, Z = SymMNA.smna(modified_net_list)

# Put matrices into SymPy 
X = Matrix(X)
Z = Matrix(Z)

# build the symbolic equations
NE_sym = Eq(A*X,Z)

# turn the free symbols into SymPy variables.
var(str(NE_sym.free_symbols).replace('{','').replace('}',''))

# construct a dictionary of element values.
element_values = SymMNA.get_part_values(network_df)

temp = ''
for i in range(shape(NE_sym.lhs)[0]):
    temp += '${:s} = {:s}$<br>'.format(latex(NE_sym.rhs[i]),latex(NE_sym.lhs[i]))

Markdown(temp)

\(0 = v_{1} \cdot \left(\frac{1}{R_{41}} + \frac{1}{R_{34}} + \frac{1}{R_{33}}\right) - \frac{v_{3}}{R_{41}}\)
\(0 = v_{2} \cdot \left(\frac{1}{R_{39}} + \frac{1}{R_{28}} + \frac{1}{R_{21}} + \frac{1}{R_{16}}\right) - \frac{v_{5}}{R_{28}} - \frac{v_{3}}{R_{21}} - \frac{v_{9}}{R_{16}}\)
\(0 = v_{3} \cdot \left(\frac{1}{R_{41}} + \frac{1}{R_{22}} + \frac{1}{R_{21}} + \frac{1}{R_{20}}\right) - \frac{v_{1}}{R_{41}} - \frac{v_{4}}{R_{22}} - \frac{v_{2}}{R_{21}} - \frac{v_{6}}{R_{20}}\)
\(0 = v_{4} \cdot \left(\frac{1}{R_{40}} + \frac{1}{R_{27}} + \frac{1}{R_{22}} + \frac{1}{R_{13}}\right) - \frac{v_{7}}{R_{27}} - \frac{v_{3}}{R_{22}} - \frac{v_{13}}{R_{13}}\)
\(0 = v_{5} \cdot \left(\frac{1}{R_{5}} + \frac{1}{R_{28}} + \frac{1}{R_{1}}\right) - \frac{v_{6}}{R_{5}} - \frac{v_{2}}{R_{28}} - \frac{v_{10}}{R_{1}}\)
\(0 = v_{6} \cdot \left(\frac{1}{R_{6}} + \frac{1}{R_{5}} + \frac{1}{R_{20}} + \frac{1}{R_{11}}\right) - \frac{v_{7}}{R_{6}} - \frac{v_{5}}{R_{5}} - \frac{v_{3}}{R_{20}} - \frac{v_{11}}{R_{11}}\)
\(0 = v_{7} \cdot \left(\frac{1}{R_{6}} + \frac{1}{R_{3}} + \frac{1}{R_{27}}\right) - \frac{v_{6}}{R_{6}} - \frac{v_{12}}{R_{3}} - \frac{v_{4}}{R_{27}}\)
\(0 = v_{8} \cdot \left(\frac{1}{R_{44}} + \frac{1}{R_{30}} + \frac{1}{R_{29}}\right) - \frac{v_{9}}{R_{44}}\)
\(0 = v_{9} \cdot \left(\frac{1}{R_{44}} + \frac{1}{R_{17}} + \frac{1}{R_{16}} + \frac{1}{R_{15}}\right) - \frac{v_{8}}{R_{44}} - \frac{v_{10}}{R_{17}} - \frac{v_{2}}{R_{16}} - \frac{v_{18}}{R_{15}}\)
\(0 = v_{10} \cdot \left(\frac{1}{R_{9}} + \frac{1}{R_{2}} + \frac{1}{R_{17}} + \frac{1}{R_{1}}\right) - \frac{v_{11}}{R_{9}} - \frac{v_{15}}{R_{2}} - \frac{v_{9}}{R_{17}} - \frac{v_{5}}{R_{1}}\)
\(I_{1} = v_{11} \cdot \left(\frac{1}{R_{9}} + \frac{1}{R_{12}} + \frac{1}{R_{11}} + \frac{1}{R_{10}}\right) - \frac{v_{10}}{R_{9}} - \frac{v_{16}}{R_{12}} - \frac{v_{6}}{R_{11}} - \frac{v_{12}}{R_{10}}\)
\(0 = v_{12} \cdot \left(\frac{1}{R_{4}} + \frac{1}{R_{3}} + \frac{1}{R_{18}} + \frac{1}{R_{10}}\right) - \frac{v_{17}}{R_{4}} - \frac{v_{7}}{R_{3}} - \frac{v_{13}}{R_{18}} - \frac{v_{11}}{R_{10}}\)
\(0 = v_{13} \cdot \left(\frac{1}{R_{43}} + \frac{1}{R_{18}} + \frac{1}{R_{14}} + \frac{1}{R_{13}}\right) - \frac{v_{14}}{R_{43}} - \frac{v_{12}}{R_{18}} - \frac{v_{20}}{R_{14}} - \frac{v_{4}}{R_{13}}\)
\(0 = v_{14} \cdot \left(\frac{1}{R_{43}} + \frac{1}{R_{32}} + \frac{1}{R_{31}}\right) - \frac{v_{13}}{R_{43}} - \frac{v_{22}}{R_{31}}\)
\(0 = v_{15} \cdot \left(\frac{1}{R_{7}} + \frac{1}{R_{25}} + \frac{1}{R_{2}}\right) - \frac{v_{16}}{R_{7}} - \frac{v_{18}}{R_{25}} - \frac{v_{10}}{R_{2}}\)
\(0 = v_{16} \cdot \left(\frac{1}{R_{8}} + \frac{1}{R_{7}} + \frac{1}{R_{19}} + \frac{1}{R_{12}}\right) - \frac{v_{17}}{R_{8}} - \frac{v_{15}}{R_{7}} - \frac{v_{19}}{R_{19}} - \frac{v_{11}}{R_{12}}\)
\(0 = v_{17} \cdot \left(\frac{1}{R_{8}} + \frac{1}{R_{4}} + \frac{1}{R_{26}}\right) - \frac{v_{16}}{R_{8}} - \frac{v_{12}}{R_{4}} - \frac{v_{20}}{R_{26}}\)
\(0 = v_{18} \cdot \left(\frac{1}{R_{38}} + \frac{1}{R_{25}} + \frac{1}{R_{24}} + \frac{1}{R_{15}}\right) - \frac{v_{15}}{R_{25}} - \frac{v_{19}}{R_{24}} - \frac{v_{9}}{R_{15}}\)
\(0 = v_{19} \cdot \left(\frac{1}{R_{42}} + \frac{1}{R_{24}} + \frac{1}{R_{23}} + \frac{1}{R_{19}}\right) - \frac{v_{21}}{R_{42}} - \frac{v_{18}}{R_{24}} - \frac{v_{20}}{R_{23}} - \frac{v_{16}}{R_{19}}\)
\(0 = v_{20} \cdot \left(\frac{1}{R_{37}} + \frac{1}{R_{26}} + \frac{1}{R_{23}} + \frac{1}{R_{14}}\right) - \frac{v_{22}}{R_{37}} - \frac{v_{17}}{R_{26}} - \frac{v_{19}}{R_{23}} - \frac{v_{13}}{R_{14}}\)
\(0 = v_{21} \cdot \left(\frac{1}{R_{42}} + \frac{1}{R_{36}} + \frac{1}{R_{35}}\right) - \frac{v_{19}}{R_{42}} - \frac{v_{22}}{R_{36}}\)
\(0 = v_{22} \cdot \left(\frac{1}{R_{37}} + \frac{1}{R_{36}} + \frac{1}{R_{31}}\right) - \frac{v_{20}}{R_{37}} - \frac{v_{21}}{R_{36}} - \frac{v_{14}}{R_{31}}\)

The symbolic solution of the network equations takes a long time, so the following code substitutes numerical values into the network equations.

NE = NE_sym.subs(element_values)

Display the equations with numeric values.

temp = ''
for i in range(shape(NE.lhs)[0]):
    temp += '${:s} = {:s}$<br>'.format(latex(NE.rhs[i]),latex(NE.lhs[i]))

Markdown(temp)

\(0 = 3.0 v_{1} - 1.0 v_{3}\)
\(0 = 4.0 v_{2} - 1.0 v_{3} - 1.0 v_{5} - 1.0 v_{9}\)
\(0 = - 1.0 v_{1} - 1.0 v_{2} + 4.0 v_{3} - 1.0 v_{4} - 1.0 v_{6}\)
\(0 = - 1.0 v_{13} - 1.0 v_{3} + 4.0 v_{4} - 1.0 v_{7}\)
\(0 = - 1.0 v_{10} - 1.0 v_{2} + 3.0 v_{5} - 1.0 v_{6}\)
\(0 = - 1.0 v_{11} - 1.0 v_{3} - 1.0 v_{5} + 4.0 v_{6} - 1.0 v_{7}\)
\(0 = - 1.0 v_{12} - 1.0 v_{4} - 1.0 v_{6} + 3.0 v_{7}\)
\(0 = 3.0 v_{8} - 1.0 v_{9}\)
\(0 = - 1.0 v_{10} - 1.0 v_{18} - 1.0 v_{2} - 1.0 v_{8} + 4.0 v_{9}\)
\(0 = 4.0 v_{10} - 1.0 v_{11} - 1.0 v_{15} - 1.0 v_{5} - 1.0 v_{9}\)
\(1.0 = - 1.0 v_{10} + 4.0 v_{11} - 1.0 v_{12} - 1.0 v_{16} - 1.0 v_{6}\)
\(0 = - 1.0 v_{11} + 4.0 v_{12} - 1.0 v_{13} - 1.0 v_{17} - 1.0 v_{7}\)
\(0 = - 1.0 v_{12} + 4.0 v_{13} - 1.0 v_{14} - 1.0 v_{20} - 1.0 v_{4}\)
\(0 = - 1.0 v_{13} + 3.0 v_{14} - 1.0 v_{22}\)
\(0 = - 1.0 v_{10} + 3.0 v_{15} - 1.0 v_{16} - 1.0 v_{18}\)
\(0 = - 1.0 v_{11} - 1.0 v_{15} + 4.0 v_{16} - 1.0 v_{17} - 1.0 v_{19}\)
\(0 = - 1.0 v_{12} - 1.0 v_{16} + 3.0 v_{17} - 1.0 v_{20}\)
\(0 = - 1.0 v_{15} + 4.0 v_{18} - 1.0 v_{19} - 1.0 v_{9}\)
\(0 = - 1.0 v_{16} - 1.0 v_{18} + 4.0 v_{19} - 1.0 v_{20} - 1.0 v_{21}\)
\(0 = - 1.0 v_{13} - 1.0 v_{17} - 1.0 v_{19} + 4.0 v_{20} - 1.0 v_{22}\)
\(0 = - 1.0 v_{19} + 3.0 v_{21} - 1.0 v_{22}\)
\(0 = - 1.0 v_{14} - 1.0 v_{20} - 1.0 v_{21} + 3.0 v_{22}\)

Solve for the node voltages.

%%time
U = solve(NE,X)

CPU times: user 254 ms, sys: 0 ns, total: 254 ms
Wall time: 257 ms

As reported by %%time, the time to get a numerical solution is very short.

Display the numerical solution.

table_header = ['unknowns', 'values','units']
table_row = []

for name, value in U.items():
    if str(name)[0] == 'I':
        unit = 'device current'
    else:
        unit = 'voltage'
    table_row.append([str(name),float(value),str(unit)])

print(tabulate(table_row, headers=table_header,colalign = ('right','decimal','left'),
    tablefmt="simple",floatfmt=('5s',',.7f','20s')))

  unknowns     values  units
----------  ---------  -------
        v1  0.0606015  voltage
        v2  0.1600000  voltage
        v3  0.1818045  voltage
        v4  0.1720301  voltage
        v5  0.2763910  voltage
        v6  0.3345865  voltage
        v7  0.2864662  voltage
        v8  0.0606015  voltage
        v9  0.1818045  voltage
       v10  0.3345865  voltage
       v11  0.5936842  voltage
       v12  0.3527820  voltage
       v13  0.2198496  voltage
       v14  0.1267669  voltage
       v15  0.2864662  voltage
       v16  0.3527820  voltage
       v17  0.3111278  voltage
       v18  0.1720301  voltage
       v19  0.2198496  voltage
       v20  0.2278195  voltage
       v21  0.1267669  voltage
       v22  0.1604511  voltage

The solution optained from LTSpice is shown below and these values agree with the Python solution above.

V(n005):     0.276391    voltage
V(n010):     0.334586    voltage
V(n015):     0.286466    voltage
V(n007):     0.286466    voltage
V(n012):     0.352782    voltage
V(n017):     0.311128    voltage
V(n006):     0.334586    voltage
V(n016):     0.352782    voltage
V(n011):     0.593684    voltage
V(n004):     0.17203     voltage
V(n013):     0.21985     voltage
V(n020):     0.22782     voltage
V(n009):     0.181805    voltage
V(n018):     0.17203     voltage
V(n002):     0.16000     voltage
V(n019):     0.21985     voltage
V(n003):     0.181805    voltage
V(n008):     0.0606015   voltage
V(n014):     0.126767    voltage
V(n022):     0.160451    voltage
V(n001):     0.0606015   voltage
V(n021):     0.126767    voltage

Since the circuit consists of only resistors and one current source, the \(A\) matrix is the Nodal Addmittance Matrix or NAM, which is oftern designated as \(Y\) in circuit analysis text books. The following code converts the SymPy matrix to a NumPy matrix. This is done because symbolic matrix inversion takes much longer than numerical inversion.

Y = np.array(A.subs(element_values), dtype=float)

The inverse of \(Y\) is the impedance matrix, \(Z\).

Z = np.linalg.inv(Y)

Driving-point impedance
The impedance at a single node \(k\) with respect to the reference node (the Thevenin impedance \(Z_{Th,k}\)), it is simply the diagonal element: \(Z_{Th,k} = Z_{kk}\). This is the impedance seen looking into node \(k\) with respect to ground (the reference node) when all independent sources are set to zero (voltage sources short-circuited, current sources open-circuited).

node_A = 11
print(f'Equalivent resistance between node {node_A:d} and ground is: {Z[node_A-1,node_A-1]:,.3f}')

Equalivent resistance between node 11 and ground is: 0.594

Transfer impedance
The transfer impedance between node \(j\) and node \(i\) is \(Z_{ji}\), if \(i \neq j\). It is the voltage at node \(i\) per unit current injected at node \(j\), with all other current injections being zero. For reciprocal networks (like those made only of resistors, capacitors, and inductors), \(Z_{kj} = Z_{jk}\). A higher transfer impedance indicates a weaker connection and less effective voltage support from that generator to the load.

node_A = 11
node_B = 19
print(f'The transfer impedance between node {node_A:d} and node {node_B:d} is: {Z[node_A-1,node_B-1]:,.4f}')

The transfer impedance between node 11 and node 19 is: 0.2198

5.4 Summary

In this chapter we examined resistive electrical circuits. The Python MNA code is useful in cases where the newtork equations in symbolic form are desired. What this chapter as shown is the following:

• Complexity vs. Method: The examples demonstrate a clear progression in circuit complexity. Circuit 1 is small enough for manual methods. Circuit 2 is a specific problem with a focus on an unconventional analysis question. Circuit 3 is highly complex (nonplanar, dependent sources), making manual analysis impractical.
• Analysis Tools: The text highlights the use of the Modified Nodal Analysis (MNA) as an algorithmic method suitable for computer implementation (like in Circuit 3 with SymPy) compared to traditional Nodal or Loop analysis, even noting that MNA can increase the number of equations (Circuit 1).
• Symbolic Solutions: For complex circuits like Circuit 3, symbolic analysis can generate correct expressions but may not provide immediate, useful insight due to their length.